Fizikai Szemle 2006/12. 420.o.
FIZIKAI MÉRÉSEK ÚTKÖZBEN
Görbe László, Piarista Gimnázium, Budapest
Nyerges Gyula, Zsigmondy Vilmos Gimnázium és Informatikai Szakközépiskola, Dorog
Sebestyén Zoltán, Pécs
Simon Péter, Leowey Klára Gimnázium, Pécs
Ujvári Sándor, Lánczos Kornél Gimnázium, Székesfehérvár
2006-tól a CERN nemzeti tanárképző programot indított,
melynek keretében a különböző országokból érkező csoportok
anyanyelvükön hallhatnak részecskefizikai előadásokat.
Európában elsőként, augusztus 20. és 26. között a
magyar fizikatanárok 38 fős csoportja (Hungarian Teachers
Programme 2006) élt ezzel a lehetőséggel. A Fizikai
Szemle idei szeptemberi számában beszámoltunk az egyhetes
program szakmai és kulturális élményeiről.
Ha sok fizikatanár van együtt, nemcsak beszélgetnek a
fizikáról, tanításról, hanem szívesen végeznek kísérletet
vagy mérést is. Az egyhetes tanfolyam során négyféle mérést
végeztünk szabadidőnkben. A mérések előkészítéséért
külön köszönet illeti a tanulmányutat is szervező Sükösd
Csabát. Ő vetette fel azt a gondolatot is, hogy az út
során méréseket végezzünk, és megbízta az ezekért felelős
kollégákat: a földrajzi helymeghatározásért Nyerges
Gyulát, a háttérsugárzás méréséért Ujvári Sándort, a víz
forráspontjának méréséért Görbe Lászlót, a légnyomás
méréséért pedig Sebestyén Zoltánt és Simon Pétert.
Földrajzi helymeghatározás
Manapság, a műholdas navigációs rendszerek korában
természetesnek tűnik, hogy tudjuk, éppen merre járunk.
Néhány évszázaddal ezelőtt azonban az utazóknak iránytű
és csillagászati mérőműszerek segítségével kellett meghatározniuk
földrajzi pozíciójukat. Ezen múlt útjuk sikere,
de sokszor az életük is. A mérések egyszerű eszközökkel
is elvégezhetők - természetesen kisebb pontossággal.
Ezeket a méréseket végeztük el a szertárban fellelhető
eszközök felhasználásával Budapest határában, röviddel
indulásunk után. A földrajzi szélesség meghatározása az
egyszerűbb feladat, csupán egy szögmérő és egy függőón
(esetünkben ez egy zsinegre kötött anyacsavar volt) kell
hozzá. A méréshez nagy méretű, táblai szögmérőt használtunk,
középpontjára már előre rögzítettük a függőt, így
ha a szögmérőnk függőleges síkban áll, a zsineg mutatja
az egyenes él függőlegestől mért eltérését (1. ábra). Nincs
más dolgunk, mint a műszer élét a Nap felé irányítani. Vetítőernyőt
helyeztünk a szögmérő mögé, és csúcsainak (az
egyenes él végpontjai) árnyékát figyelve mozgattuk a
szögmérőt. Ha a két pont árnyéka egybeesik, az él éppen
jó irányba mutat, és a skáláról leolvashatjuk a Nap zenittávolságát.
A mérést célszerű a tavaszi vagy az őszi napforduló
idejére időzítenünk, ekkor ugyanis a Nap éppen az
égi egyenlítőn delel, a leolvasott szög ilyenkor a földrajzi
szélességünkkel egyenlő. Az év más napjain sajnos bonyolultabb
a helyzet, ilyenkor ismernünk kell a Nap deklinációját
(egyenlítő fölötti/alatti látószögét) és ezt az értéket
hozzá kell adnunk mérési eredményünkhöz. Utunk
során mi is így jártunk el, a kérdéses szöget a Csillagászati
Évkönyv táblázatából nyertük. A másik szükséges adat a
Nap delelési időpontja, ennek meghatározásához viszont
szükségünk van a földrajzi hosszúságra. Ennek hiányában
folyamatosan kell a mérést végeznünk, és azt az adatot
kell felhasználnunk, amikor a legmagasabbra hágott a
Nap útja során. A delelés környékén szerencsére a Nap a
horizonttal párhuzamosan jár, így a mérés nem érzékeny
az időpont pontos meghatározására. A delelés bekövetkezését
egy iránytű segítségével is meghatározhatjuk, mint
később látni fogjuk, ezt a módszert követtük mi is. A szögmérő
fokos beosztással bír, ez határozza meg mérésünk
pontosságát. A szögmérő segítségével a Nap zenittávolságát
36°-nak mértük, ezt korrigálva a Nap 12°-os deklinációjával
48°-os szélességet kapunk.
A földrajzi hosszúság meghatározása lényegesen bonyolultabb
feladat, először az észak-déli irányt kell kitűznünk.
Vízszintes papírlapon rajzoljunk É-D-i vonalat
iránytű segítségével! (Mi előre megrajzoltuk a vonalat, és
tájolóval forgattuk a lapot a megfelelő irányba.) A vonal
déli végére állítsunk függőleges pálcát! (Esetünkben ez
egy átfúrt fakorongba helyezett ceruza volt, de a rögzítés
készülhet gyurmából is.) Mind a vízszintes, mind a függőleges
irányt ellenőrizzük vízmérték segítségével!
(Lényegesen pontosabban is kitűzhetjük az É-D-i
irányt indiai kör segítségével: Rajzoljunk kört a függőleges
pálca talppontja köré, majd jelöljük meg azt a két
pontot, ahol a pálca végének árnyéka délelőtt, illetve
délután áthalad rajta! A két pont éppen K-Ny-i irányt
határoz meg, erre kell merőlegest szerkesztenünk a talpponton
keresztül. Utazók lévén mi a gyorsabb, tájolós
megoldást választottuk.)
Ezután azt kell megmérnünk, hogy a pálca árnyéka
mikor halad át a vonalon. Az év négy napján (április 15.,
június 13., szeptember 1., és december 25.) a Nap éppen
délben delel, ekkor célszerű ezt a mérést elvégezni.
Augusztus lévén a mi mérésünket az időegyenlet aktuális
értékével korrigálni kellett. (Az időegyenlet grafikonja
megtalálható többek között a Távcso világa című kötetben
is.) Azt kell megállapítanunk, hogy a delelés hány
perccel később (nyugati féltekén korábban) következik
be a világidő szerinti (greenwichi) délnél. (Hazánkban 1,
nyári időszámítás idején 2órával mutatnak többet az
órák.) Az eredményt 4-gyel osztva (4 percenként tesz
meg 1 fokot a Nap égi útján) megkapjuk a keresett
hosszúságot. Ennél a mérésnél a legnagyobb bizonytalanságot
a délvonal kitűzése okozza, hiszen tájolóval
pusztán 1-2fok pontossággal tudjuk beállítani az É-D-i
irányt. További hibaforrás a lap vízszintes és a pálca függőleges
iránytól való eltérése, valamint az időpont leolvasási
bizonytalansága. A halmozott hibák akár 5-6 fokos
eltérést is okozhatnak. Megmértük a pálca magasságát
(189 mm) és az árnyék hosszát (142mm) is a deleléskor
(2. ábra). A két adat ismeretében tangenstáblázat segítségével
szintén meghatározható a Nap delelési magassága
(~37°), ebből pedig az észlelőhely földrajzi szélessége
(49°) is. A Nap delelése 12:40 (10:40 UT) körül következett
be. Mintegy 80 perccel dél előtt. Ezek szerint a 20.
keleti hosszúság körül mértünk. (A valódi koordináták:
47°28'N és 18°52'E voltak.)
Ez a kísérlet nem igényel túl nagy előkészületet, viszont
szabadban, osztálykirándulás során akár több, egymással
versengő csoportban is elvégezhető. Azt a csoportot,
amelyik a legjobb eredményt éri el,
valamilyen jutalomban is részesíthetjük.
A tanulók motiváltságát,
és a Természethez "fizikusi"
szemmel való hozzáállását erősítheti.
Víz forráspontjának mérése
Mint tanulmányainkból tudjuk,
a víz forráspontja függ a külső
nyomástól. Ezt kísérlettel igen
könnyű igazolni. Sokáig forraljunk lombikban vizet, majd
dugaszoljuk le és kezdjük vízzel locsolva hűteni. A megjelenő
buborékok jelzik, hogy a víz újra forr. Ebben az
állapotban nehéz megmérni a víz hőmérsékletét, bár biztos,
hogy kevesebb, mint 100 Celsius fok. Ha a tengerszint
feletti magasság nő, akkor csökken a légnyomás, s
így a víz forráspontjának értéke is változik. A CERN-ben
eltöltött tanulmányút alkalmat adott ennek tanulmányozására.
Mivel különböző magasságokban voltunk, így
több magasságban is - borszeszhőmérő és elektromos
hőmérő, gázmelegítő, csapvíz és ásványvíz felhasználásával
- megmértük a víz forráspontját (3. ábra).
Eredmények
A kapott eredményeket az 1. táblázat tartalmazza. Az
alkoholos hőmérő (ami biztonságosan szállítható volt)
szerint nem sokkal a tengerszint felett 96 fokon forr a víz.
Ahogyan egyre magasabbra megyünk, úgy csökken a forráspont.
(A hegyre ugyanazt a csapvizet vittük, amivel
lent a mérést végeztük). Érdekes, hogy a CERN-ben ivóvízként
szolgáló víz forráspontja alacsonyabb, mint a
csapvízé.

Levonható következtetések
- A mérési bizonytalanságot itt már növelheti az,
hogy nem a teljes hőmérő volt a vízben.
- A forráspont meghatározása nem volt olyan pontos
(és közben más okok miatt is változhatott a légnyomás),
hogy a tengerszint feletti kis magasságváltozásokat is
érzékelni tudjuk.
- Arra a napra, amikor a Mont Blanc-on jártunk, ciklon
érkezését jelezték, s ez délután meg is érkezett. Ez is
befolyásolhatta a légnyomást, és csökkenthette a víz forráspontját.
- A víz forráspontjának változása a magassággal talán
több kísérletet is megérdemelne.
| 1. táblázat |
| A víz forráspontja különböző tengerszint feletti magasságokban |
| időpont | helyszín | magasság | víz |
forráspont
borszeszhőmérővel |
forráspont
elektromos
hőmérővel |
| augusztus 28. | Budapest | 110 m | csapvíz | 96 °C | - |
| augusztus 25. | CERN | 530 m | csapvíz | 96 °C | - |
| augusztus 25. | CERN | 530 m | ásványvíz | 94 °C | - |
| augusztus 26. | Chamonix | 1020 m | csapvíz | 92 °C | 94 °C |
| augusztus 28. | Mont Blanc | 3840 m | csapvíz | 84 °C | 86 °C |
A légnyomás mérése
A pisai kertészek a következő problémával fordultak
annak idején Galileihez: szárazság idején azt tapasztalták,
hogy a szívó-nyomó kutak segítségével nem lehet a
vizet a kútból 10 méter fölé emelni. Az idős tudós egyik
kedvenc tanítványának, Torricellinek adta át a problémát
megoldásra. A jelenség magyarázatának keresése
közben a fiatal tudós, Viviani segítségével megmérte a
légnyomás értékét. Az iskolákban ma is szívesen tanított
kísérlet szerint a légnyomás körülbelül 76 cm magas higanyoszloppal
tart egyensúlyt, ami körülbelül 10 méter
magas vízoszlop nyomásának felel meg. A tanulmányút
során két alkalommal mértük meg a légnyomást, persze,
vizet használva. A mérések elvégzésére természetesen
csak úgy kerülhetett sor, hogy még otthon gondosan
előkészítettük, s kipróbáltuk azokat. Félvödörnyi
vízbe 11 méter hosszú, vastag falú, 1 cm átmérőjű átlátszó
műanyagcsövet tekertünk föntről lefelé. Eközben a
cső megtelt vízzel. A csövet lejtősen és lassan kellett a
víz alá tolni, hogy ne kerüljön bele buborék, ezután a
cső felső végére a víz alatt egy körülbelül 30 cm hosszú,
egyik végén lezárt és vízzel teletöltött üvegcsövet szorítottunk,
s elkezdtük emelni. Egy bizonyos magasság elérésekor
a víz a cső végénél gyöngyözni, majd hevesen
buborékolni kezdett. Ezt igen tisztán lehetett látni az
üvegcsövecskében. (Műanyagcsőben nem látszik ilyen
szépen a jelenség!). Érdekes volt megfigyelni az alacsony
(16 °C, ill. 3 °C) hőmérsékletű forrást, mely a cső
felső részében uralkodó alacsony nyomásnak volt köszönhető.
Ekkor egy picit vártunk, hogy a vízben oldott
gázok kiforrjanak a vízből. Ez alatt egyre lejjebb került a
csőben a vízszint. Most elszorítottuk hermetikusan egy
pillanatszorítóval a vízszint alatt 1-2cm-rel a műanyagcsövet,
s megint emeltünk rajta. Ez a trükk sokat javított
a mérés pontosságán. Most már megmérhettük a vízoszlop
magasságát. A mérés elvégzésében a csoport lelkesen
segített kettőnknek.
1. mérés
2006. augusztus 25-én 8 órakor a CERN meyrini campusa
38-as épület külső lépcsőházában (4. ábra), a tengerszint
feletti magasság 426 m (± 10 m), hőmérséklet
+16 °C = 289 K. Mért érték: h = 928 cm.
Értékelés: Az első gondolatunk az lehet, hogy ez az
érték jelentősen eltér a fizikaórákról ismert tíz métertől.
(Nálunk volt egy még otthon hitelesített Fischer márkájú
barométer, ami 982kPa-t mutatott. Ez valóban 10 méter
magas vízoszlop nyomását jelenti.) Ne felejtsük el, hogy a
vízoszlop felett most nem a higany esetében jelen levő
Torricelli-űr (10-3 torr) van jelen, hanem telített vízgőz.
16 °C hőmérsékleten a telített vízgőz nyomása körülbelül
1700 Pa, ami 17,3 cm magas vízoszlopnak felel meg. Az
így mért érték 5,5%-kal van a barométer által jelzett érték
alatt. A hiba több forrásból is származhat. Egyrészt a csőben
minden bizonnyal maradt még némi levegő, másrészt
a hosszúság mérése is igen pontatlan volt.
2. mérés:
2006. augusztus 26-án 12 órakor 3842 m tengerszint
feletti magasságon: a Mont Blanc Aiguille du Midi csúcsán
(5. ábra). A levegő hőmérséklete +2 °C = 275 K. Mért érték:
h = 636 cm. Hőmérsékletváltozás: 14 °C = 14 K.
Értékelés: A nálunk lévő barométer ilyen alacsony
légnyomást már nem képes mérni, ezért a barometrikus
magasságformulát hívom segítségül.
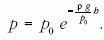
A p0 értékének az előző napi, a campuson műszerrel mért
értéket veszem, p0 = 982hPa. A magasság, h = 3842 - 426 m
= 3416 m, a levegő sűrűsége, 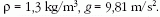 .
A barometrikus magasságformula ugyan állandó hőmérsékletű
gázoszlopra szól, most mégis használhatjuk jó közelítésnek,
hisz a hőmérsékletváltozás 5% alatt van.
Ezek után a formula alkalmazásával p = 630,2hPa, ami
642 cm vízoszlopot jelent. A számolt és mért érték közötti
6 cm eltérés 1%-nál kevesebbet jelent. Ez zavarba ejtően
pontos érték. (Ha figyelembe vesszük a +2 °C-hoz tartozó
telített vízgőz nyomását, ami körülbelül 7 cm, akkor
igazán elégedettek lehetünk.)
.
A barometrikus magasságformula ugyan állandó hőmérsékletű
gázoszlopra szól, most mégis használhatjuk jó közelítésnek,
hisz a hőmérsékletváltozás 5% alatt van.
Ezek után a formula alkalmazásával p = 630,2hPa, ami
642 cm vízoszlopot jelent. A számolt és mért érték közötti
6 cm eltérés 1%-nál kevesebbet jelent. Ez zavarba ejtően
pontos érték. (Ha figyelembe vesszük a +2 °C-hoz tartozó
telített vízgőz nyomását, ami körülbelül 7 cm, akkor
igazán elégedettek lehetünk.)
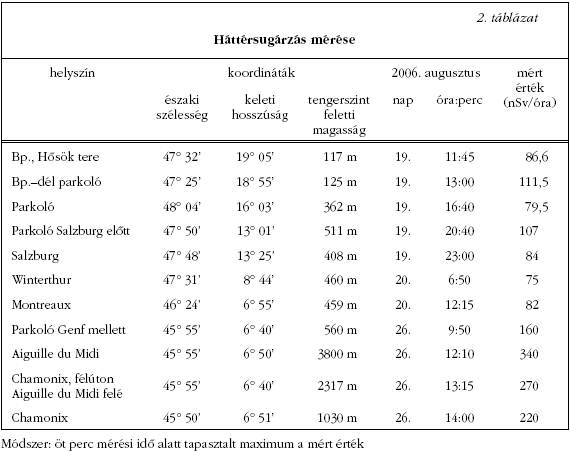
Háttérsugárzás mérése
A magyar fizikatanárok CERN-beli továbbképzése során
az előre meghatározott program szerint gammadózis-teljesítmény-
mérést is végeztünk. A mérési adatokat az oda- és
visszaúton, valamint Meyrin városában, a CERN székhelyén
vettük fel (2. táblázat ). A dózisteljesítmény hely
szerinti változását regisztráltuk. GPS segítségével határoztuk
meg a földrajzi koordinátákat és a tengerszint feletti
magasságot. Másik műszerünk egy dózisteljesítmény-mérő
volt, amelyik indítás után folyamatosan, másodpercenként
mintát véve azonnal kiírta az eredményt.
Az utazás során a helyszínek többségét a véletlen döntötte
el, ott mértünk, ahol a csoport pihenőt tartott. Az
általunk választott hely pedig a CERN telephelye és a
Mont Blanc egyik csúcsa, az Aiguille du Midi volt.
A mérés módszerét meghatározta az, hogy az alacsony
intenzitású háttérsugárzásból jött beütésszámok statisztikus
fluktuációja nagy, és ezért a műszer kijelzése is állandóan
ingadozott. A digitális kijelzés átlagát nehéz lett volna
meghatározni, ezért minden helyszínen 5 percig bekapcsolva
tartottuk a műszert, és az ezen idő alatt mutatott
maximális értéket tekintettük eredménynek. A mérés
alapján a dózisteljesítmény összefüggést mutat a tengerszint
feletti magassággal. Minél magasabban végeztük a
mérést, annál nagyobb volt a dózisteljesítmény, ami a kozmikus
sugárzás értékének növekedését jelenti. A mérések
kis száma természetesen nem engedi meg túl messzemenő
következtetések levonását. A program részeként többek
között meglátogattuk az Atlas-kísérlet helyszínét, ahol
egy 60 m mély alagútban lehetett volna mérést végezni, de
a műszert a szállodában felejtettük. Itt a mélyben érdekes
lett volna megmérni az árnyékolás hatását, de ez sajnos a
mérést végző hibájából elmaradt. Amit sikerült megtudni:
a genfi emberek egy évben átlagosan 8 mSv dózist kapnak, míg
az alagútban dolgozó magyar
fizikus személyi dozimétere 6
mSv-et mutatott az egész évre
átszámolva. Ezt az elmaradt,
alagútbeli mérést a következő
csoportnak érdemes lesz elvégeznie.
A CERN-i tanulmányút során
végzett mérések mindegyikének
megvolt ugyan a kijelölt
felelőse, mégis a csoport minden
tagja aktívan részt vett a
megvalósításukban. A fent leírt
mérések elvégzése önmagában
is örömet okozott mindannyiunknak,
és ötleteket, bátorítást
adott ahhoz, hogy diákjainkkal
is elvégeztessük ezeket szakkörök,
osztálykirándulások alkalmával.
Hiszen mérni jó, és a
Természet ezernyi érdekes, mérni
valójelenséget kínál.






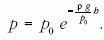
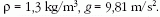 .
A barometrikus magasságformula ugyan állandó hőmérsékletű
gázoszlopra szól, most mégis használhatjuk jó közelítésnek,
hisz a hőmérsékletváltozás 5% alatt van.
Ezek után a formula alkalmazásával p = 630,2hPa, ami
642 cm vízoszlopot jelent. A számolt és mért érték közötti
6 cm eltérés 1%-nál kevesebbet jelent. Ez zavarba ejtően
pontos érték. (Ha figyelembe vesszük a +2 °C-hoz tartozó
telített vízgőz nyomását, ami körülbelül 7 cm, akkor
igazán elégedettek lehetünk.)
.
A barometrikus magasságformula ugyan állandó hőmérsékletű
gázoszlopra szól, most mégis használhatjuk jó közelítésnek,
hisz a hőmérsékletváltozás 5% alatt van.
Ezek után a formula alkalmazásával p = 630,2hPa, ami
642 cm vízoszlopot jelent. A számolt és mért érték közötti
6 cm eltérés 1%-nál kevesebbet jelent. Ez zavarba ejtően
pontos érték. (Ha figyelembe vesszük a +2 °C-hoz tartozó
telített vízgőz nyomását, ami körülbelül 7 cm, akkor
igazán elégedettek lehetünk.)