Fizikai Szemle honlap

Tartalomjegyzék

Fizikai Szemle 2006/12. 412.o.

KOMPLEX KRISTÁLYMORFOLÓGIÁK MODELLEZÉSE HÁROM DIMENZIÓBAN

Pusztai Tamás, Bortel Gábor, Tóth Gyula, Gránásy László
MTA Szilárdtestfizikai és Optikai Kutatóintézet, Budapest

A mindennapi életünkben előforduló kristályos anyagok jelentős része polikristályos, azaz nagyszámú kristályszemcséből épül fel. A polikristályos anyag fizikai tulajdonságai nagymértékben függenek az alkotó kristályszemcsék méret és összetétel szerinti eloszlásától, melyet a kristálycsíraképződés és -növekedés viszonya határoz meg. A polikristályos megszilárdulás leírásához tehát olyan elméletre van szükség, amely alkalmas mindkét folyamat leírására. Előző cikkünkben egy olyan, viszonylag egyszerű kontinuum leírást mutattunk be, melynek keretében sikeresen modellezhetők igen bonyolult kétdimenziós polikristályos megszilárdulási alakzatok [1]. A cikk megjelenése óta kidolgoztuk fázismezőmodellünk háromdimenziós általánosítását [2, 3]. A jelen írásban az új modell által nyújtott egyedülálló lehetőségeket szeretnénk illusztrálni.

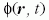Mivel kiindulópontunk a korábbiakban ismertetett kétdimenziós fázismezőmodell, felidézzük annak néhány alapvető vonását. A lokális fizikai állapotot hely- és időfüggő skalármezőkkel jellemezzük. Így a szilárd-folyadék átmenet leírására a keplet fázismezőt vezetjük be, melynek értéke egy és nulla között változik a kristály-folyadék határfelületen keresztül [1, 4-7]. A fázismező olyan, a kristályban jelenlevő szerkezeti tulajdonság, amely eltűnik a folyadékban (pl. a részecskesűrűség domináns Fourier- komponensének amplitúdója). Többnyire két- vagy többkomponensű folyadék megszilárdulására vagyunk kíváncsiak, ezért további jellemzőként szerepelhetnek a lokális kémiai összetételt meghatározó - 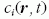keplet - koncentrációmezők, melyek időfejlődése (a kémiai diffúzión, illetve reakciókon keresztül) befolyásolhatja a kristályosodás folyamatát. A kristályosodó folyadék szabadenergiája több tagból tevődik össze. A tömbi fázisok összetétel- és hőmérsékletfüggő szabadenergiáján felül figyelembe kell vennünk a fázismező térbeli változásához rendelhető járulékot is, melyet a gradiensnégyzet közelítés keretében tárgyalunk (ebből a tagból ered a felületi szabadenergia). A tömbi szabadenergia a lehetséges kristály-, illetve folyadékállapotok számától függően legalább két minimummal rendelkezik, melyek a makroszkopikusan megvalósuló stabil és metastabil fázisoknak felelnek meg. Kristályosodás során a rendszer a túlhűtött (metastabil) folyadéknak megfelelő lokális minimumból a stabil kristályos fázisnak megfelelő mélyebb minimumba kerül, miközben át kell jutnia e két minimum közti szabadenergia-gáton. Homogén túlhűtött folyadékból kiindulva erre csak a termikus fluktuációk figyelembevételével nyílik mód. Az átalakulás időbeli lefutását tehát az egyes mezők időfejlődését meghatározó nemlineáris mozgásegyenletek, a bennük szereplő mobilitások (melyek a transzlációs, illetve kémiai diffúziós együtthatókkal hozhatók kapcsolatba), illetve a termikus fluktuációkat reprezentáló zaj tulajdonságai együttesen határozzák meg. Ez utóbbiakat a fluktuáció- disszipáció tétel határozza meg.

1.ábra/1 1.ábra/2 1.ábra/3
1. ábra. Véletlen orientációjú kristályok homogén nukleációja és dendrites növekedése Al50,8Ti49,2 olvadékban a kifejlesztett polikristályos fázismező elmélet szerint. A számolás 480 x 480 x 480 rácson, köbös kristályszimmetriák és periodikus határfeltétel mellett történt. A felületi szabadenergia anizotrópiája 2,5%-os volt. A különböző szürke árnyalatok különböző kristálytani orientációkat jelölnek.

Több kristály egymással versengő növekedésekor meg kell különböztetnünk a különféle kristálytani orientációkat, azaz meg kell adnunk, hogy az egyes kristályszemcsék esetén a kristálysíkok hogyan állnak a laboratóriumi rendszerhez képest. Két dimenzióban ez a Kobayashi és munkatársai [8] által bevezetett orientációs mező segítségével tehető meg. Amennyiben azt is feltesszük, hogy a szilárd fázisban az orientációs tér változásához tartozó szabadenergia-járulék arányos az orientációs mező gradiensének abszolútértékével, éles szemcsehatár és az orientáció szögkülönbségével arányos szemcsehatárenergia adódik, ami elfogadható közelítés kis és közepes szögű szemcsehatároknál.

Kobayashi és munkatársai [8] csak a kristályos fázisban értelmezték az orientációs mezőt. Valójában a kristályos rend, és ennek részeként a kristálytani orientáció is (azaz, hogy milyen irányban állnak az adott kristály síkjai)fokozatosan alakul ki a kristály-folyadék határrétegben. E jelenség leírásához az orientációs mezőt a folyadéktartományokon is értelmeztük [1, 4-7], ahol a lokális orientáció időben és térben korrelálatlanul ingadozik, amit az orientációs mozgásegyenlethez adott zaj biztosít. Ehhez az alábbi fizikai kép rendelhető: Amennyiben megkeressük azt az irányt, melynél a kristályos elsőszomszéd-környezet a legjobban hasonlít a vizsgált folyadékmolekula környezetére (pl. szögkorrelációt vizsgálunk), minden egyes folyadékmolekulához hozzárendelhető egy pillanatnyi orientáció. Ez az orientáció térben és időben folyamatosan ingadozik. Azt, hogy a pillanatnyi illeszkedés mennyire jó, a másik szerkezeti rendparaméter, a fázismező aktuális értéke tükrözi. A kristályosodási fronton áthaladva a folyadékbeli véletlenül ingadozó lokális orientáció fokozatosan beáll az adott kristályszemcsét jellemző irányba. Az orientációs szabadenergia általunk javasolt formája biztosítja, hogy az orientációs rendeződés a fázismező változásával (a kristályosodással) szinkronban lép fel, míg a szilárd fázisban visszakapjuk az orientációs szögkülönbséggel arányos szemcsehatár-energiát.

Az orientációs mező időfejlődését leíró mobilitás az orientációs egyensúly kialakulásának időskáláját meghatározó úgynevezett rotációs diffúziós állandóval hozható kapcsolatba. Komplex molekuláris folyadékokban, alacsony hőmérsékleten, a rotációs diffúziós együttható jelentősen lecsökken a növekedési sebességet meghatározó transzlációs diffúziós együtthatóhoz képest. Ennek tulajdonítható a polikristályos növekedési mintázatok megjelenése nagy túlhűtéseknél. A gyorsan haladó megszilárdulási fronton nincs mód a tökéletes orientációs rend kialakulására: orientációs hibák, szemcsehatárok fagynak be a kristályos fázisba. Ezen elképzelések alapján kétdimenziós modellünk segítségével a polikristályos alakzatok széles spektrumát reprodukáltuk [1, 4-7].

A három dimenzióra történő általánosítás azonban nem egyszerű. Szemben a kétdimenziós esettel, ahol egyetlen szög megadása elegendő egy kristálysík orientációjának rögzítéséhez, három dimenzióban három szög szükséges: a kristálysíkok normálisának iránya két szöggel adható meg. Azonban ezen tengely körül még egy további szöggel elforgatható a kristály. Definiálnunk kell emellett a két kristályszemcse közti orientációkülönbség mértékét is. Ehhez, az általánosság megszorítása nélkül, rendeljünk derékszögű koordinátarendszereket a kristályokhoz. A szemcsék orientációját jelképező két koordinátarendszer egymásba vihető egyetlen jól meghatározott tengely körüli forgatással. Az orientációbeli különbség mérésére ezen forgatás szögét választjuk. Ezek után viszonylag egyszerűen megadható az orientációs szabadenergia olyan megfogalmazása, melyben (a) a szemcsehatár-energia arányos az orientáció fentiek szerint definiált szögkülönbségével, és (b) melyből a kétdimenziós határesetben visszakapjuk korábbi modellünket. További figyelmet igényel a kristályszimmetriák kezelése: Ha két kristályszemcse szimmetriaművelettel egymásba vihető, akkor kontinuum modellünkben nem képződhet közöttük szemcsehatár. Ezt az orientációs mozgásegyenlet megoldása során vesszük figyelembe.

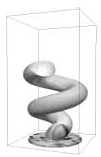
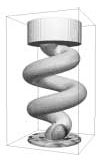
2.ábra/1 2.ábra/2 2.ábra/3 2.ábra/4
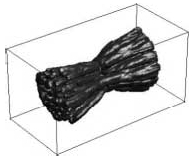
2. ábra. Egykristály szerkezeti elemek öntésére szolgáló orientációszelektor fázismezőmodellje. A megszilárdulás felületi nukleációval indul a modell alján. A spirális nyakba csak néhány orientáció jut be, és csak egyetlen orientáció jut keresztül lehetővé téve, hogy a szerkezeti elem (a felső részen található henger) egykristályként szilárduljon meg. A különböző szürke árnyalatok különböző kristálytani orientációnak felelnek meg. A számolás 200 x 200 x 400-as rácson, köbös kristályszimmetriák és periodikus határfeltétel mellett történt. A felületi szabadenergia anizotrópiája 2,5%-os volt.

A fentieknek megfelelően egy kétalkotós olvadék kristályos megszilárdulásának leírására csatolt, sztochasztikus parciális differenciálegyenleteket oldunk meg numerikusan, periodikus határfeltétel mellett. Ehhez párhuzamos számítógépes kódot fejlesztettünk ki, melynél a szimulációs ablakot olyan térbeli tartományokra osztjuk, amelyet egy-egy számítógép-processzor kezel. A szükséges számítási kapacitás biztosítására egy 61 és egy 121 processzorból álló személyi számítógép "fürtöt" építettünk fel az MTA Szilárdtestfizikai és Optikai Kutatóintézetében. Az utóbbi egység számítási teljesítménye ~0,5 teraflop (azaz 0,5 · 1012 lebegőpontos művelet másodpercenként). A háromdimenziós fázismező-szimulációk meglehetősen számításigényesek, így például az 1. ábrán látható szimuláció, melyet ~110,6 millió rácsponton végeztünk, közelítőleg egy hétig futott 100 processzoron.

A szimuláció során homogén, túlhűtött folyadék a kezdőállapot. A kristályos fázis megjelenése a kétdimenziós esethez hasonló módon [1], a termikus fluktuációkat modellező zaj hozzáadásával, véletlen helyen véletlen orientációval létrejövő csírák kialakulásával történik. Amennyiben nincsenek idegen felületek a rendszerben, a csíraképződés (nukleáció) a folyadék saját termikus fluktuációival - homogén módon - történik. Az idegen felületek elősegíthetik a kristálycsíra képződést, mely esetben heterogén nukleációról beszélünk. Minthogy a homogén csíraképződés valós körülmények között szinte sosem fordul elő, és a gyakorlat számára érdekes esetekben a kristálycsíraképződés a konténerfalakon, illetve idegen részecskék felületén heterogén módon történik, módszert dolgoztunk ki a heterogén nukleáció leírására. A nukleációval létrejött kristálycsírák tovább növekednek. Az ennek során fellépő diffúziós instabilitások és az anizotrópia összjátéka következtében bonyolult, úgynevezett dendrites alakzatok jöhetnek létre, melyek ágai jól meghatározott kristálytani irányokban nőnek (részletesebben ld. [1]). A modellünk által nyújtott lehetőségeket néhány látványos polikristályos mintázat létrejöttének folyamatán keresztül szemléltetjük. (Honlapunkon további információ kapható a fenti modellek részleteiről [9].)

  1. )A fentiekben említett homogén csíraképződés és dendrites növekedés útján történő megszilárdulás folyamata látható az 1. ábrán. A szimulációkban kialakuló dendrites morfológia igen hasonló a kísérletekben megfigyelthez, és az időfejlődést leíró kinetikus (Avrami-Kolmogorov) exponens is közel áll a kísérleti értékekhez.
  2. )Az egykristályelemek előállítására széles körben használt eszköz, az orientációszelektor ("pigtail"= malacfarok) működését illusztrálja a 2. ábra. A megszilárdulás a minta alján felületi (heterogén) csíraképződéssel indul, s így kezdetben számos eltérő orientációjú kristályszemcse verseng egymással. A spirálisan kanyarodó orientációszelektoron (folyadékkal töltött csatornán) azonban már csak egyetlen orientáció jut keresztül, lehetővé téve egykristályelemek készítését.
  3. )A kétdimenziós esethez hasonlóan, megfelelő körülmények között bonyolult polikristályos növekedési formák jönnek létre három dimenzióban is. Ezek a mintázatok egykristálycsírából erednek, de növekedésük során újabb és újabb kristályszemcsék képződnek a peremükön. Az eltérő orientációjú új szemcsék kialakulása kétféle módon is elérhető: i)Idegen részecskéket adalékolunk az olvadékhoz;
    ii)Lecsökkentjük az orientációs és fázismező mobilitások arányát.     Mindkét mechanizmus alkalmas arra, hogy az egykristály dendrites morfológiát polikristályos gömbszerű, úgynevezett szferolitikus (gömbszerű, részben vagy teljesen kristályos) alakzattá változtassuk (3. ábra). A morfológiai átmenet oka a következő. Bár a dendrites forma kialakulásához szükséges anizotrópia végig jelen van, az (i) esetben az idegen részecskék növekvő száma miatti zavar, míg a (ii) esetben a relatíve lassú orientációs rendeződés miatt fellépő orientációs hibák (szemcsehatárok) befagyása a kristályba csökkenti a szemcseméretet, aminek következtében egyre kevésbé érvényesül az anizotrópia hatása.
  4. )Az orientációs mobilitás csökkentésével analóg módon hat a növekedési morfológiára a termodinamikai hajtóerő (túlhűtés vagy túltelítés) növekedése. Ekkor a kristályosodási front haladási sebessége megnő, így nagyobb számban kerül sor az orientációs hibák szilárd fázisba történő befagyasztásával képződő új szemcsék kialakulására. A túltelítés növelésével a tűszerű egykristály- növekedési forma fokozatosan átmegy a radiálisan növekvő szemcsékből álló térkitöltő, szferolitos alakzatba (4. ábra). Megjegyzésre méltó, hogy a szferolitos növekedési forma egyike a talán legáltalánosabb polikristályos alakzatoknak. Megfigyelték öntöttvasban (szferolitos grafitszemcsék), fém- és oxidüvegekben, polimerekben, biopolimerekben. Szferolitos szerkezű lehet például a vesekő, az inzulinkristályok, vagy az érfalon képződő koleszterinlerakódás, de a csokoládéban is kialakulhatnak ilyen struktúrájú kristályszemcsék.

3.ábra/1 3.ábra/2 3.ábra/3 3.ábra/4
3.ábra/5 3.ábra/6 3.ábra/7 3.ábra/8
3. ábra. Morfológiai átmenet az egykristály dendrites szerkezet és a szferolitos polikristályos alakzat között. A felső sorban az idegen részecskék részecskesűrűsége balról jobbra 0, 0,6, 0,8 és 1,0 (tetszőleges egységekben). Az alsó sorban az orientációs mobilitás értéke szorzódik az alábbi faktorokkal: 1,00, 0,20, 0,15 és 0,10. A különböző szürke árnyalatok különböző kristálytani orientációknak felelnek meg. A számolás 200 × 200 × 200 rácson, köbös kristályszimmetriák és periodikus határfeltétel mellett történt. A felületi szabadenergia anizotrópiája 2,5%-os volt.

A polikristályos fázismező-elmélet csoportunk által kidolgozott háromdimenziós általánosítása lehetővé teszi a természetben és a laboratóriumokban előforduló bonyolult polikristályos mintázatok kialakulásának modellezését. Termodinamikai adatbázisokkal és az olvadékok áramlását leíró hidrodinamikai kódokkal összekapcsolva modellünk hozzájárulhat a tudományos igényű anyagtervezés megalapozásához. A fenti kutatásokon alapuló mikroszerkezeti szimulációk fontos részét képezik az Európai Unió 6. keretprogramja által támogatott IMPRESS projektnek, valamint két, az Európai Űrügynökség/Magyar Űrkutatási Iroda által finanszírozott, ESA PECS pályázatnak, melyek célja gazdaságosabb gázturbinák, javított tulajdonságú mágneses és kompozit anyagok, valamint környezetbarát csapágyanyagok kifejlesztése, az ehhez szükséges elméleti/gyakorlati tudás létrehozása.

4.ábra/1 4.ábra/2 4.ábra/3 4.ábra/4
4. ábra. Átmenet tűkristályból a polikristályos szferolitmintázatba a túltelítés növelésével. A szimulációk 200 × 200 × 200, illetve 200 × 400 × 200 rácsokon monoklin szimmetria és a fázismező mobilitásának erős aszimmetriája mellett történtek. Balról jobbra a túltelítés értéke rendre S = 0,76, 0,86, 0,88 és 0,90.

A szerzők köszönetüket fejezik ki Iglói Ferencnek és Tegze Györgynek a kéziratukkal kapcsolatos kritikai megjegyzéseikért és észrevételeikért.

A fenti vizsgálatok az EU FP6 IMPRESS projekt (NMP3-CT-2004- 500635), és OTKA (T037323, K62588), valamint ESA PECS (98005, 98021) pályázatok támogatásával történtek. Pusztai Tamás és Bortel Gábor kutatásait Bolyai János ösztöndíj segítette.

Irodalom
  1. . GRÁNÁSY L., PUSZTAI T., BÖRZSÖNYI T.: A polikristályos megszilárdulás térelméleti modellezése - Fizikai Szemle 55 (2005) 203-211
  2. . T. PUSZTAI, G. BORTEL, L. GRÁNÁSY: Phase field theory of polycrystalline solidification in three dimension - Europhysics Letters 71 (2005) 131-137
  3. . T. PUSZTAI, G. BORTEL, L. GRÁNÁSY: Phase field modelling of polycrystalline freezing - Materials Science and Engineering A 413-414 (2005) 412-417
  4. . L. GRÁNÁSY, T. BÖRZSÖNYI, T. PUSZTAI: Nucleation and bulk crystallization in binary phase field theory - Physical Review Letters 88 (2002) 206105-1-4
  5. . L. GRÁNÁSY, T. PUSZTAI, J.A. WARREN, J.F. DOUGLAS, T. BÖRZSÖNYI, V. FERREIRO: Growth of "dizzy dendrites" in a random field of foreign particles - Nature Materials 2 (2003) 92-96
  6. . L. GRÁNÁSY, T. PUSZTAI, T. BÖRZSÖNYI, J.A. WARREN, J.F. DOUGLAS: A general mechanism of polycrystalline growth - Nature Materials, 3 (2004)645-650.
  7. . L. GRÁNÁSY, T. PUSZTAI, J.A. WARREN: Modelling polycrystalline solidification using phase field theory - Journal of Physics: Condensed Matter 16 (2004) R1205-R1235
  8. . R. KOBAYASHI, J.A. WARREN, W.C. CARTER: Vector-valued phase field model for crystallization and grain boundary formation - Physica D 119 (1998) 415-423
  9. . http://www.szfki.hu/~grana/crystal.html