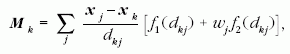Fizikai Szemle 2007/6. 201.o.
SEJTEK ÖNSZERVEZŐDÉSÉNEK FIZIKÁJA
Czirók András
ELTE TTK, Biológiai Fizikai Tanszék
Önszerveződés és kollektív viselkedés
Egy sok alkotóelemből álló rendszert általában legalább
két szerveződési szinten vizsgálhatunk. Az alkotóelemek
és a köztük fennálló kölcsönhatások alkotják
a mikroszkopikus szintet. A rendszer egészének
viselkedését egy makroszkopikus leírással jellemezhetjük,
ami a mikroszkopikus leírástól lényegesen
különböző fogalmakat használ. Egy klasszikus fizikából
vett példával élve, a nemesgázokat a mikroszkopikus
szinten jó közelítéssel az atomok között ható
van der Waals-kölcsönhatás és a Lennard-Jones-potenciál
írja le. Makroszkopikus szinten a gázt termodinamikai
állapotjelzőkkel és a köztük fennálló állapotegyenlettel
jellemezzük. A két szint között a statisztikus
fizika teremti meg a kapcsolatot. A mikroszkopikus
és makroszkopikus leírások együttes alkalmazása
- esetleg további szerveződési szintekkel bővítve -
számos, nem fizikai rendszer esetén is célravezetőnek
bizonyul. Így, különböző fogalmakkal dolgozik a
szervetlen kémia, a biokémia, a sejtbiológia és a szövettan.
A mikroszkopikus, makroszkopikus jelzőket
az alábbiakban ilyen értelemben, két különböző szerveződési
szint megkülönböztetésére fogjuk használni.
Általában egy rendszer makroszkopikus viselkedése
nem következik egyszerűen az alkotóelemek mikroszkopikus
kölcsönhatásainak ismeretéből. A két
szerveződési szint kapcsolata, a mikroszkopikus kölcsönhatások
következtében megjelenő makroszkopikus
viselkedés, az önszerveződés, sokszor intenzív
kutatás tárgya. Kollektív viselkedés alatt általában
ennek az általános problémának a következő speciális,
egyszerűbb esetét értjük. Ha a rendszert sok hasonló
alegység építi fel, akkor az alkotóelemek kollektív
viselkedése a közöttük ható kölcsönhatások miatt
alakul ki, és lényegesen különbözik attól, amit a
kölcsön nem ható elemek mutatnának.
Az autópályán spontán kialakuló sűrűséghullámok
és tranziens forgalmi dugók jó példák a nem fizikai
rendszerben fellépő kollektív viselkedésre. A rendszert
mikroszkopikus szinten az egymás után haladó
autók alkotják. Dinamikájukat részben fizikai törvények,
részben a vezetők preferenciái és reakciói határozzák
meg. Makroszkopikus szinten a rendszert hidrodinamikai
változókkal, azaz sűrűség- és sebességtérrel
írhatjuk le. A spontán forgalmi dugók nagy sűrűség
esetén alakulnak ki - egyfajta instabilitásként -
az autók közötti kölcsönhatások "melléktermékeként".
Nyilvánvaló, hogy a bedugult állapot lényegesen
különbözik a vezetők (mikroszkopikus szintű)
preferenciáitól.
A fizikán kívüli önszervező jelenségek tanulmányozása
azonban több ponton különbözik a fizikában
megjelenő kollektív jelenségek vizsgálatától. A fizikai
rendszereknél általában már jól ismerjük a kölcsönható
egységeket - a mikroszkopikus szintet - és így elegendő
csak a speciális, kollektív makroszkopikus jelenséget
vizsgálni. Ezzel szemben a biológiában általában
már a mikroszkopikus egységek (fehérjék, sejtek,
organizmusok) is rendkívül összetettek, és viselkedésük
kevéssé ismert vagy jól definiálható. Ezért a biológiai
önszervező jelenségek vizsgálatánál gyakran az alkotóelemek
releváns viselkedésére és kölcsönhatásaira is
hipotéziseket kell felállítanunk, majd az egész modellt
mérésekkel tesztelnünk. Az élő szervezetben fellépő
önszerveződés vizsgálata általában sokkal több feltételezésre
épül, mint a kollektív fizikai rendszerek tanulmányozása.
Mindenesetre, amint az alábbi példák mutatják,
a biológiai rendszerek önszerveződésének vizsgálata
számos esetben gyümölcsöző lehet.
Biokonvekció
Az önszerveződő biológiai viselkedés egy viszonylag
egyszerű példája a mikroorganizmusok (algák és baktériumok)
nagy sűrűségű tenyészeteiben megfigyelhető
folyadékáramlási mintázat. Vízben élő mikroorganizmusok
gyakran összegyűlnek a vízfelszín közelében.
Ezt a folyamatot vagy az oxigéngradiens érzékelése
és a magasabb oxigéntartalmú területek irányába
történő elmozdulás (kemotaxis ), vagy a fény felé
úszás (fototaxis) hajtja. Mivel a mikroorganizmusok
sűrűsége nagyobb a vízénél, felszíni rétegződésük
egy hidrodinamikailag instabil sűrűséginverzió. A
sűrűséginverzió Rayleigh-Taylor-instabilitást eredményez,
és a nagyobb sűrűségű folyadék különálló oszlopokban
lesüllyed (1. ábra). A mikroorganizmusok
folyamatos felfelé úszása azonban képes újra létrehozni
a sűrűséginverziót, és így a kísérletekben egy
fennmaradó áramlási mintázat alakul ki.
A rendszer makroszkopikus viselkedését a folyadék
v sebességtere, p nyomáseloszlása valamint a
mikroorganizmusok térbeli eloszlását leíró c sűrűségtér
jellemzi. A mikroorganizmusok mozgására tett feltételezések
(diffúzió, kemotaxis, fototaxis) megjelennek
mint a mikroorganizmusok J áramát leíró makroszkopikus
egyenlet speciális tagjai:
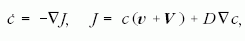 |
(1) |
ahol a mikroorganizmusok véletlenszerű mozgását a
D diffúziós állandó reprezentálja, míg V a mozgásukban
megjelenő "drift"-komponens. Fototaxis esetében
ez függőlegesen felfelé mutat, kemotaxis esetében
pedig az oxigéngradiens irányába. A folyadékdinamika
és a mikroorganizmusok kölcsönhatása egyrészt az
(1) egyenletben szereplő cv konvektív tagként, másrészt
a Navier-Stokes-egyenletben egy, az egyedsűrűség-
térrel arányos, térfogati erőként jelenik meg:
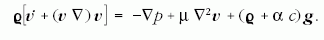 |
(2) |
A rendszer kollektív viselkedése az így kapott
egyenletrendszer numerikus vagy analitikus vizsgálatával
tanulmányozható.
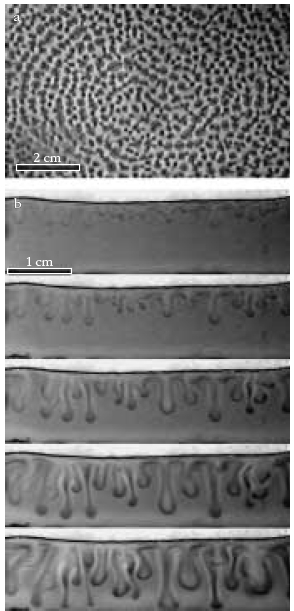
1. ábra Biokonvenció Bacillus
subtilis folyadékkultúrás tenyészeteiben. a: Petricsészében kialakuló
mintázat felülnézete. b: Hele-Shaw-cella oldalnézete és az instabilitás
időfejlődése fél perces időfelbontással. A sötétebb területeken nagyobb a
baktériumok száma [1] alapján.
Különlegesen nagy mikroorganizmus-sűrűség esetén
már nem elegendő csak az egyedsűrűség és a folyadék
makroszkopikus áramlási terének a kapcsolatát
vizsgálni. Ilyenkor a mikroorganizmusok már közvetlenül
is befolyásolják egymás mozgását: geometriai
kényszerek hatására rendeződnek, illetve érzékelhetik
a szomszédaik által keltett áramlási teret is. A létrejövő
különleges, örvénylő áramlási mintázat tulajdonságai
ma még kevéssé ismertek (2. ábra). Figyelemre
méltó ugyanakkor, hogy hasonló áramlási kép alakulhat
ki nagyon különböző biológiai rendszerekben,
kétdimenziós felületen mozgó sejtektől kezdve egészen
az állatcsordák vagy halrajok dinamikájáig. Ez
arra utal, hogy a kollektív makroszkopikus viselkedés
kialakításában a rendszer mikroszkopikus tulajdonságainak
nagy része lényegtelen.
Embrionális erek és sejthálózatok
Az önszerveződés koncepciója a biológiai szövetek
kialakulásának megértésében is hasznos lehet. Tudjuk,
hogy a genetikai állomány nem egy tervrajzhoz
hasonló módon kódolja az organizmus térbeli szerkezetét
- forma és funkció valahogy a sejtek kölcsönhatásai
következtében jön létre. A kialakuló szerkezet
azonban sokkal jobban meghatározott, mint a mikroorganizmusok
telepei, elsősorban a sokrétű, génexpressziós
mintázatokat is magukban foglaló visszacsatolások
miatt. Az egyedfejlődés során speciális gének
expressziója definiálja az embrió különböző részeit és
egyben behatárolják az ott található sejtek lehetséges
"viselkedését".
 |
 |
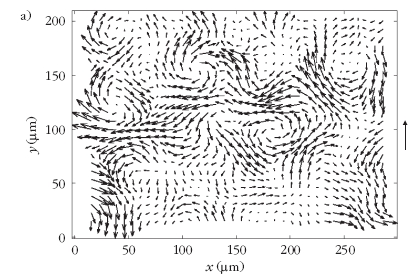
| 2. ábra. Önhajtott részecskék kollektív áramlása. a: Nagy sűrűségű
Bacillus subtilis folyadékkultúrában kísérletileg megfigyelt sebességtér
([2] alapján). b: Önhajtott részecskék hidrodinamikai modelljében
megfigyelhető tranziens örvények ([3] alapján). |
Úgy gondoljuk azonban, hogy léteznek olyan
struktúrák is, amelyeket nem közvetlenül a génexpressziós
mintázatok határoznak meg. Ilyen kollektív
mintázatképződésre lehet jó példa a melegvérű gerincesekben
megjelenő korai érhálózat, amit több
száz endotél sejt alakít ki az embriófejlődés első szakaszaiban
(3. ábra ). A sejtek véletlenszerű helyeken
differenciálódnak (születnek), gyorsan aggregátumokba
csoportosulnak, nyúlványokat növesztenek,
majd hálózatot képeznek. A mechanizmus önszervező
voltát főleg az támasztja alá, hogy az egyes szegmensek
elhelyezkedése nagyfokúegyedi változatosságot
mutat, másrészt nem azonosítottak az egyes
szegmensek jelenlétével vagy hiányával korreláló genetikai
mutációkat.
 |
 |
|
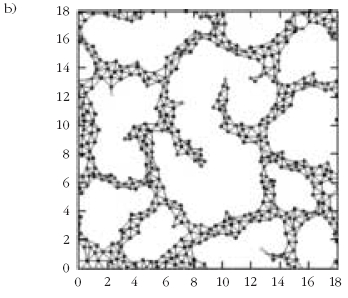
3. ábra. Embrionális érhálózat mikroszkópos képe (a) és modellje
(b), [4] alapján.
|
Munkatársaimmal felállítottunk és számítógépes
szimulációkkal alátámasztottunk egy hipotézist,
amely szerint a hálózatformálás során az érsejtek
mozgása a szomszédos sejtek mechanikai állapotától
függ. A modell a mikroszkopikus szinten, kölcsönható
sztochasztikus folyamatokként írja le a rendszert: a
k-adik sejtet ebben a közelítésben csak az xk (t ) pozíció
és a vk (t) sebesség jellemzi. A sejtmozgást egy
perzisztens véletlen bolyongással írjuk le,
ahol 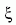 egy korrelálatlan fehér zaj, a sejt-sejt kölcsön-
hatások pedig az M determinisztikus "drift"-tagban jelennek
meg. Feltételezzük, hogy a sejt-sejt kölcsönhatások
párkölcsönhatások összegére bonthatók, és
ezek csak a két sejt távolságától függenek:
egy korrelálatlan fehér zaj, a sejt-sejt kölcsön-
hatások pedig az M determinisztikus "drift"-tagban jelennek
meg. Feltételezzük, hogy a sejt-sejt kölcsönhatások
párkölcsönhatások összegére bonthatók, és
ezek csak a két sejt távolságától függenek:
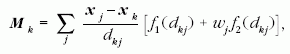 |
(4) |
ahol az összegzés a k-adik sejt szomszédaira történik,
és dkj = | xk?xj |.
Az f1 taszítás biztosítja, hogy a sejtek
ne tudjanak áthaladni egymáson. Az f2 vonzó kölcsönhatás
fejezi ki azt, hogy a sejtek szeretnek összetapadni.
Ez a kölcsönhatás a w súlyfaktoroknak megfelelően
aszimmetrikus, azaz a párkölcsönhatás két résztvevője
különböző nagyságú vonzó hatást észlelhet. Ez, a fizikai
rendszerekkel ellentétben, azért lehetséges, mert itt
nem mechanikai erőkről van szó, hanem véletlenszerű
aktív mozgást végző részecskék (sejtek) mozgásiránypreferenciáiról.
Feltételezzük, hogy a sejtek nagyobb
valószínűséggel migrálnak elnyújtott sejtek szomszédságába.
Ennek a migrációs preferenciának az lehet az
oka, hogy az elnyújtott sejtek mechanikai feszültség
alatt vannak, ezért merevebbek. Ez az elképzelés összhangban
van számos korábbi kísérleti adattal, amelyek
arra utalnak, hogy a merevebb környezet sok sejttípus
számára vonzó migrációs célpont.
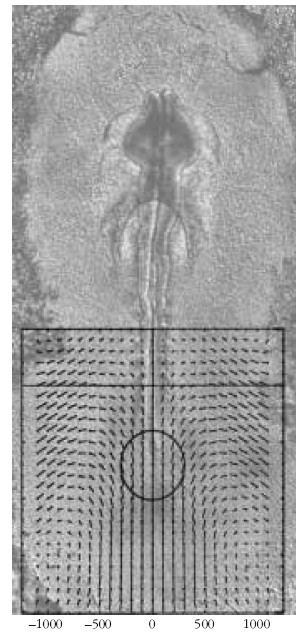
4. ábra. Korai madárembriók fejlődése során megfigyelhető szövetmozgások
sebességtere. A rácspontokból kiinduló szakaszok a szövetmozgás
irányát és nagyságát mutatják ([5] alapján).
A (3) és (4) egyenletek numerikus integrálásával
megmutatható, hogy a modell valóban képes hálózatok
létrehozására, és az időfejlődése sok szempontból
tükrözi a kísérletileg tapasztaltakat. Bár a modellt még
számos ponton kísérletileg ellenőrizni kell, a mintázatképződés
kollektív jelenségként történő értelmezése
hasznos koncepciónak bizonyul. Az érfalakat alkotó
sejtek önszervező viselkedésének megértése -
hasonló vizsgálatokon keresztül - szükséges a mesterséges
szövetek előállítására tett kísérletekhez is.
Szövetmechanika: erők és relaxáció
A még nagyobb skálájú anatómiai struktúrák kialakulását
kísérő sejt- és szövetmozgások szisztematikus
felderítése az elmúlt évtizedben vált lehetővé, részben
a specifikus fluoreszcens jelölő molekulák és a számítógép-
vezérelt optikaimikroszkópia-technikák elterjedése
révén. A sejtek szövetalkotása nemcsak a fejlődésbiológia
egyik klasszikus problémája, hanem a
mesterséges szövetek létrehozásának (tissue-engineering)
egyik alapvető kérdése is.
A fejődés korai szakaszában a gerinces embriók szerkezete
drámai módon átalakul: egy látszólag forgásszimmetrikus
felületen először egy tengely, a primitív
csík alakul ki. Ezzel egyidőben elkezdődik a gasztruláció,
a hólyagcsíra képzése. A gasztruláció során sejtek
vándorolnak a primitív csíkon keresztül az embrió belsejébe,
és kialakítják a középső (mezodermális) csíralemezt.
Bár a gasztruláció különböző szakaszai már régóta
ismertek, a szövetformálódás kinetikájáról és dinamikájáról
napjainkban kapjuk az első mérési adatokat
(4. ábra). Mivel a szövet is egy fizikai test, mozgását és
deformációit mechanikai erők okozzák. Ezeket az erőket
az embrió sejtjei fejtik ki, tehát itt is egy olyan rendszerünk
van, ahol a mikroszkopikus skálán történő sejtdinamika
(mozgás, kontraktilitás) létrehozza a makroszkopikus
skálájú szövetmozgásokat. A sejtek által kifejtett
erők kapcsolata a szövetet formáló erőkkel és a
deformált szövetben felhalmozódó mechanikai feszültséggel
azonban még jórészt ismeretlen.
Szilárd testek és folyadékok esetében nyíráskor
mechanikai feszültség lép fel, de egy közönséges
(newtoni) folyadékban, például vízben, a nyírófeszültség
a nyírás megszűnésekor azonnal eltűnik. A
folyadék molekuláihoz hasonlóan, mozgásukkal a sejtek
is hatékonyan le tudják csökkenteni a kialakuló
mechanikai feszültséget úgy, hogy megbontják a sejt-
sejt kapcsolatokat. Ehhez az aktív átrendeződéshez
azonban több időre van szükségük mint a vízmolekuláknak.
Sejtaggregátumokon végzett mérések arra
utalnak, hogy ez a relaxációs idő közelítőleg tíz perc,
ami nem elhanyagolható a szövetmozgások órás időskálájához
képest. Tehát, a sejtaggregátumok és így,
feltételezhetően, az egyszerű embrionális szövetek is
nem-newtoni folyadéknak tekinthetők - olyanok mint
a polimeroldatok. Jelenleg a terület egyik legnagyobb
kihívását az jelenti, hogy a fenti megfontolások alapján
állítsuk fel az embriogenezis olyan mechanikai
modelljét, amelyben a szövetek kísérletileg megfigyelhető
mozgásai visszavezethetőek különböző sejtcsoportok
által kifejtett erőkre.
Kitekintés
Összefoglalásként megállapíthatjuk, hogy a sejt- és szövetműködés
megértése egy rendkívül érdekes probléma,
hiszen a sok komponensből álló rendszerek viselkedése
még az alkotóelemek részletes ismeretében sem
jósolható meg egyszerűen. Mivel a különböző skálájú
folyamatok integrálása gyakran megoldhatatlan
valamilyen kvantitatív elemzés nélkül, számos sejtbiológiai
probléma vizsgálatában ötvöznek molekuláris biológiai,
statisztikai, műszaki vagy fizikai módszereket.
Irodalom
Jánosi M., Czirók A., Silhavy D., Holczinger A.: Is bioconvection
enhancing bacterial growth in quiscent environments? Environmental
Microbiology, 4 (2002) 525-531.
Dombrowski C., Cisneros L., Chatkaew S., Goldstein R.E., Kessler
J.O.: Self-Concentration and large-scale coherence in bacterial
dynamics. Physical Review Letters, 93 (2004) 098103.
Csahók Z., Czirók A.: Hydrodynamics of bacterial motion. Physica
A, 243 (1997) 304.
Szabó A., Perryn E.D., Czirók A.: Network formation of tissue
cells via preferential attraction to elongated struc tures. Physical
Review Letters, 98 (2007) 038102.
Czirók A., Rongish B.J., Little C.D.: Extracellular matrix dynamics
during vertebrate axis formation. Developmental Biology, 268
(2004) 147-157.
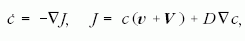
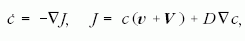
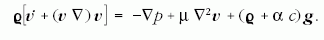






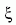 egy korrelálatlan fehér zaj, a sejt-sejt kölcsön-
hatások pedig az M determinisztikus "drift"-tagban jelennek
meg. Feltételezzük, hogy a sejt-sejt kölcsönhatások
párkölcsönhatások összegére bonthatók, és
ezek csak a két sejt távolságától függenek:
egy korrelálatlan fehér zaj, a sejt-sejt kölcsön-
hatások pedig az M determinisztikus "drift"-tagban jelennek
meg. Feltételezzük, hogy a sejt-sejt kölcsönhatások
párkölcsönhatások összegére bonthatók, és
ezek csak a két sejt távolságától függenek: