Fizikai Szemle honlap

Tartalomjegyzék

Fizikai Szemle 2007/6 216.o.

HÁLÓZATOK MINDENÜTT

Karinthy Frigyest legtöbben humoros és más szépirodalmi írásai révén ismerik. Talán kevesen tudják róla, hogy már középiskolás korában élénken érdeklődött a matematika és a természettudományok iránt. Ez az érdeklődése megmaradt később is, és 1929-ben a Minden másképpen van gyűjteményben egy kimondottan matematikai kérdésről írt Láncszemek címmel. Vajon hány közvetlen ismeretségi kapcsolaton keresztül lehet összekötni valamelyikünket egy távoli helyen élő másik emberrel? Másképpen megfogalmazva: az emberek ismeretségi hálójában maximum hány lépésen keresztül lehet két, véletlenszerűen kiválasztott embert összekapcsolni? A példa kedvéért próbálja meg az Olvasó saját maga és egy eszkimó között megtalálni a legrövidebb utat közvetlen ismerősökön (és barátokon, családtagokon) keresztül. Könnyen lehet, hogy az Olvasónak van egy sokat utazó ismerőse, akinek az egyik munkatársa járt messze északon és találkozott az adott eszkimóval.

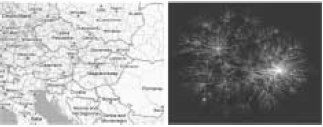
1. ábra
1. ábra. Az úthálózatot városok alkotják és egy városnak általában 3-4szomszédja van, de 10 vagy több szomszéddal rendelkező várost nem találunk. Az internet egymással összekötött számítógépekből áll, és gyakoriak a kiugróan sok szomszéddal rendelkező pontok, az ábrán világosabb színnel. (Az ábrák forrása a Google Maps, illetve a http://www.caida.org weboldal.)

Így az Olvasótól az utazó ismerősén és annak munkatársán keresztül három lépés vezet a kiválasztott eszkimóhoz. Karinthy becslése szerint az összes (akkoriban másfél milliárd) ember közül bármelyik kettő összeköthető legfeljebb 5 lépésben. Frissebb becslések szerint napjainkban ez a szám valahol 6 és 9 között van, azaz az ismeretségi hálóban két résztvevő között a távolság (a legrövidebb úthossz) jóval kisebb, mint az összes résztvevő száma. Általánosságban az ilyen tulajdonságú hálózatokat - az ismeretségi háló alapján - kis világnak hívjuk.

Karinthy példája csupán egy a sok hálózat (gráf) közül, amely körülvesz minket. Mindannyian ismerjük a világméretű számítógép-hálózatot, az internetet, és a számítógépeken tárolt weboldalak hálóját, a www-t. Legtöbben naponta telefonálunk, és ha a telefonhívásokat ábrázoljuk, akár csak egyetlen telefontársaság előfizetői között, akkor is több millió pontból álló gráfot kapunk. Ennek a gráfnak a (csúcs)pontjai az előfizetőket jelölik, a csúcsokat összekötő vonalak (élek) pedig azt, hogy két előfizető között volt-e hívás. Hosszabb időszak alatt természetesen többször is telefonálhat egymásnak két ember, ilyenkor az adott kapcsolatot ábrázoló élnek nagyobb súlyt adhatunk. A felsorolt példák közül a www és a telefonhívások gráfjában is rendelhetünk irányt az élekhez, ezekkel a nyilakkal a hiperlinkek, illetve a hívások irányát tudjuk jelölni.

Az emberi kapcsolatok és az elektronikus rendszerek mellett a biológiában is számos hálózat ismert. A legtöbb biológiai hálózat azt összegzi, hogy egy rögzített sejttípusban a különböző molekulák (például fehérjék és anyagcseretermékek) a reakcióik során milyen más molekulákkal lépnek kapcsolatba. Egy ilyen "kölcsönhatási térkép" tartalmazza például azt, hogy a vizsgált sejttípusban a víz- és a glükózmolekula között van-e kölcsönhatás. Ha igen, akkor a két molekulát ábrázoló egy-egy pont össze van kötve. Az emberi nyelvek és maga az emberi gondolkodás is sok hálót produkál. Könyvespolcokon gyakran megtalálható a magyar és az angol nyelvű szinonimaszótár; az ebben lévő kapcsolatok definiálják a szinonimahálózatot. Szintén hasznos eszköz a könyvtárak által a könyvek osztályozásához, besorolásához használt egységes tizedes osztályozás (ETO). Az ETO-ban minden témanevet egy számsor jelöl, amelynek az elemeit tizedespontok választják el. Ha ezt lerajzoljuk, akkor egy nagy elágazó fát kapunk (szintén hálózat), amelynek a legalsó csúcspontjain általános címszavak találhatók, például 1. szépirodalom, 2. történetírás, majd ezek felett a fa kisebb ágain egyre speciálisabbak a témanevek: 1.1. regény, 1.2. vers stb. A közlekedésből is ismerünk hálókat, például a közúti hálózatban mindegyik város egy pont és két pontot összekapcsolunk, ha a két város egy főút mentén szomszédos. A légi közlekedésben szintén a városok a pontok (bár egy városnak több repülőtere is lehet), és két várost összekötünk, ha van köztük közvetlen repülőjárat.

A matematikusok a gráfokat több száz éve vizsgálják, és a gráfelmélet a matematika egyik igen jelentős ága. Azonban az utóbbi egy évtizedben a hálózatokról rendelkezésre álló adatok mennyisége és részletgazdagsága ugrásszerűen megnőtt. Ezt a jelentős változást felerősítette az internet fejlődése, amely korábban nem látott mennyiségű mérési adatot tett ingyenesen elérhetővé bárki számára. Emiatt a matematikusokon kívül a fizikusok, biológusok, szociológusok és más kutatók is egyre intenzívebben kapcsolódnak be a hálózatok kutatásába. Ezen belül a fizikusok a nagy és összetett (komplex) rendszerek megfigyelése során mindig az egyszerű, közös tulajdonságokat keresik. Sokszor nem a pontos egyezést vizsgálják, hanem csak a gyakran előforduló (statisztikai értelemben vett) hasonlóságot. Ezért a 90-es évek végétől kezdődően a fizikusok, más kutatókkal együtt, meglepve és örömmel tapasztalták, hogy a sokféle komplex hálózatban több egyszerű, hasonló tulajdonság található. Az egyik legkorábbi ilyen eredmény, hogy a nagy hálózatok közül sok rendelkezik az ismeretségi hálózatban már látott kisvilág - tulajdonsággal. Szintén kis világ az internet és a www, viszont nem kis világ egy pókháló és a közúti hálózat. A legkisebb számú lépést, amellyel egy gráfban két csúcs az éleken haladva összeköthető, a két pont közötti legrövidebb úthossznak nevezzük. A kisvilág-tulajdonság matematikai megfogalmazásban azt mondja ki, hogy ha növeljük egy hálózat méretét, akkor a benne mérhető legrövidebb úthosszak a hálózat méreténél jóval lassabban (legfeljebb logaritmikusan) nőnek. Azaz, ha egy kisvilághálózatban a csúcsok (résztvevők) száma tíz- vagy százszorosára nő, a legrövidebb út bármely két pont között akkor is csak egy vagy két lépéssel lesz hosszabb.

2. ábra
2. ábra. A gyümölcslégy (Drosophila melanogaster) fehérjéinek kölcsönhatási hálózatára vonatkozó első részletes "térkép" 2004-ben készült el. Az emberi sejtek fehérjéi közötti kölcsönhatások térképe ilyen részletességgel még nem ismert. Azonban a gyümölcslégy fehérjéi között talált kölcsönhatások segítségével, szekvenciahasonlóság alapján az emberi fehérjék kölcsönhatásai is pontosabban jósolhatóak. (Az ábra forrása: Giot et.al., Science, 302 [2004] 1727-1736.)

A legrövidebb utak vizsgálata után most nézzük meg azt, hogy vajon egy kiválasztott csúcspontból nézve másmilyennek látjuk-e a www-t és az úthálózatot (1. ábra). A www-n és az úthálózatban is sok olyan pont (weboldal, város) található, amelyiknek kevés kapcsolata van (hiperlinkkel kapcsolt másik weboldal, illetve szomszédos város). Azonban, ha a sok kapcsolattal rendelkező pontokat vizsgáljuk, akkor a két hálózatban jelentős eltérést tapasztalunk. Egy városnak általában 3-4közúti szomszédja van, de 10-nél semmiképp sem több. Viszont a weboldalak között soknak van ezernél is több kapcsolata és néhánynak, mint a Google és a Yahoo, több millió. Egy csúcs szomszédainak számát az adott csúcs fokszámának nevezzük. A különböző fokszámok eloszlásfüggvénye, p (k ), megmutatja, hogy ha az összes csúcs közül véletlenszerűen kiválasztunk egyet, akkor annak a fokszáma p (k ) valószínűséggel lesz k. Az úthálózatban nagyon kis eséllyel találunk olyan csúcsot, amelynek a fokszáma az átlagos értéknél jóval nagyobb; az útvonalak gráfján és a hasonló hálózatokban végzett mérések szerint ez a valószínűség a k értékkel exponenciálisan csökken:

Putak(k) ~ e-k.

A www-n és a biológiai hálózatokban gyakoriak az átlagosnál jóval több kapcsolattal rendelkező csúcsok. A mérések szerint ezekben a hálózatokban a fokszámeloszlás a nagy fokszámoknál hatványfüggvény szerint csökken:

Pwww(k) ~ k-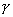képlet.

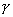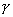Itt képlet általában 2 és 3 közötti szám. Ha például képlet = 3, akkor a k = 10 fokszámú csúcs előfordulási valószínűsége 8-szor kisebb, mint a k = 5 fokszámú csúcsé. Ezzel szemben az exponenciális esetben a k = 10-es csúcs e5-szer (körülbelül 150-szer) kevésbé gyakori, mint a k = 5-ös. A nagy fokszámú csúcsok előfordulási valószínűsége alapján a hálózatokat két fő csoportba szokás sorolni. Az exponenciális hálózatokban az átlagosnál jóval több kapcsolattal rendelkező csúcsokat nem találunk (az exponenciális függvény nagyon gyorsan csökken), míg a hatványfüggvény szerinti fokszámeloszlású, más néven skálafüggetlen hálózatokban ehhez képest gyakoriak a kiugróan sok szomszéddal rendelkező csúcsok.

A fokszámeloszlás és a kisvilág -tulajdonság sok alkalmazásban igen fontos szerephez jut. A www-n és a légi közlekedésben alapvető, hogy néhány lépéssel (kattintással, illetve átszállással) a hálózatban bárhová eljuthassunk. De ezért a jó tulajdonságért mindkét esetben árat kell fizetnünk. A www-n gyakran előfordul, hogy a legtöbb kapcsolattal rendelkező oldalakat egyszerre próbálja sok felhasználó letölteni, a légi közlekedés pedig lehetőséget ad arra, hogy távoli vidékek fertőző betegségei gyorsan eljussanak mindenhová. Érdekes, hogy az elmúlt években az ezekkel kapcsolatos jelenségekre a statisztikus fizika elméleti eszközeivel igen pontos leírásokat és javaslatokat sikerült adni.

Napjainkban az egyik legaktívabban kutatott hálózat az élő sejtek fehérjéinek kölcsönhatási hálózata. Sok ismert szekvenciájú és szerkezetű fehérjéről még nem vagy csak részben ismert, hogy milyen feladatot végez a sejtben. A hálózatban vele kölcsönható más fehérjék (szomszédok) segítségével azonban ez a funkció jósolható. További érdekesség, hogy a fehérjék általában csoportosan, összekapcsolódva végeznek el egy-egy feladatot. A fehérje-fehérje kölcsönhatási hálózat segítségével új fehérjecsoportokat találhatunk, és jobban megismerhetjük, hogy ezek a csoportok (fehérjemodulok) hogyan működtetik az emberi, állati és növényi sejteket (2. ábra).

Farkas Illés
MTA-ELTE Biológiai Fizika Kutatócsoport
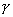