Fizikai Szemle honlap |
Tartalomjegyzék |
Vancsó Péter, Biró László Péter, Márk Géza István
MTA Műszaki Fizikai és Anyagtudományi Kutatóintézet
Nanoszerkezetek Osztály
A kvantummechanika ismerete alapvető fontosságú, hogy megértsük a körülöttünk lévő természetet, annak működését. Az elektronok mozgásának, az atomok és molekulák tulajdonságainak leírásához a klasszikus fizika törvényei (már) nem elegendőek. Habár az a mikroszkopikus méret- és időtartomány, amelyben a kvantummechanika törvényei érvényesek, távol esik emberi világunk méret- és időskálájától, ez a tudomány mégsem csupán a kutatók birodalma. A 21. század elején az embereket a mindennapokban körülvevő modern technikai eszközök [1] - például tranzisztor, lézer - működésének megértésénél is nélkülözhetetlenek a kvantummechanikai ismeretek. Ezeknek az ismereteknek az átadása az oktatás feladata, legyen szó középiskolai vagy egyetemi szintű oktatásról [2].
A kvantummechanika oktatása az egyik legnehezebb feladat a fizika tanítása folyamán, mivel a diákok túl absztraktnak, matematikailag túl bonyolultnak tartják [3]. Ez érthető is, ha végiggondoljuk, hogy a klasszikus fizika fogalomkörének és törvényeinek megértésénél segítségünkre vannak mindennapi tapasztalataink, mindenki által könnyen elvégezhető kísérletek. Ezzel szemben a kvantummechanika mérettartományában végzett mérések többnyire közvetettek és nehezen értelmezhetők.
Matematikai szempontból ahhoz, hogy klasszikus mechanikai leírását adjuk egy részecske (tömegpont) mozgásának, 6 paramétert kell megadnunk: r(t) és p(t), azaz a hely és a lendület x, y és z komponensét az idő függvényében. Ezek határozzák meg a többi dinamikai változót, például az energiát. A Newton-törvények ismeretében kiszámíthatjuk az r(t) és p(t) függvények értékeit minden pillanatra, ha ismerjük a függvények értékét valamely tetszőleges t0 kezdeti pillanatban, azaz adottak az r0 = r(t0) és p0 = p(t0) kezdeti hely- és lendületértékek, továbbá ismerjük a részecskére hatóerőket. A kvantummechanikai leírásmód ennél bonyolultabb. A részecske állapotát t pillanatban egy hullámfüggvény adja meg, Ψ(r, t), amely tartalmazza az összes információt, amit a részecskéről tudni lehet. Látható tehát, hogy a 6 paraméter helyett, most végtelen számú paraméterünk van: a Ψ 3 + 1 = 4 változós függvény értékei a tér minden pontjában, minden időpontban. A Ψ(r, t) függvényt valószínűségi amplitúdónak nevezzük, mert
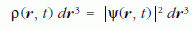
annak a valószínűségét adja meg, hogy a részecske t időpontban egy r pont körüli dr3 térfogatelemben található, ρ(r, t ) pedig a megtalálási valószínűségsűrűség. A hullámfüggvény időfejlődését az időfüggő Schrödinger-egyenlet írja le, amely egy homogén lineáris parciális differenciálegyenlet:
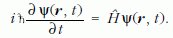
Ez az az egyenlet, amely mai ismereteink szerint az atom- és molekulafizika, a szilárdtestfizika, sőt a kémia és a biológia összes (nem-relativisztikus) jelenségét kormányozza. Következményeit számtalan kísérlet igazolta az egyenlet megalkotása óta eltelt több, mint 80 év folyamán.
A Schrödinger-egyenlet determinisztikus; adott Ψ0(r) = Ψ(r, t = t0) kezdőállapot esetén a hullámfüggvény kiszámíthatóbár mely t időpontra. A véletlenszerűség, az indeterminizmus, a fizikai mennyiség mérése folyamán jelenik meg a kvantummechanikában. A Schrödinger-egyenlet megoldásához a kezdő állapot ismeretén kívül szükséges az adott fizikai rendszert meghatározó H Hamilton-operátor. Konzervatív rendszerek esetén H = K+V, ahol K a kinetikus, V pedig a potenciális energia operátora, tehát a rendszert végső soron a V potenciáloperátor írja le. Ha ez a potenciál lokális, akkor a potenciális energia operátor hatása egy egyszerű V(r) potenciálfüggvénnyel adható meg.
Látható tehát, hogy a kvantummechanika matematikai nyelvezetének megértése szintén nem egyszerű feladat, és további probléma, mint említettem, hogy a jelenségeket nem tudja a diák a mindennapi tapasztalataihoz kapcsolni - Ψ(r, t ) komplex értékű függvény(!) -, a mérések pedig mindig közvetettek: maga a hullámfüggvény nem mérhető, csak a belőle származtatott mennyiségek, az úgynevezett megfigyelhető mennyiségek, mint például <r>, a hely várhatóértéke:
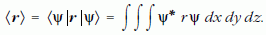
Ahhoz, hogy mégis szemléletes képet tudjunk adni a diákoknak a Schrödinger-egyenlet "működéséről", egy nagyon hasznos eszközt alkalmazhatunk: a számítógépes szimulációt. A mai személyi számítógépek sebessége és tárolókapacitása már bárki számára lehetővé teszi egyszerű kvantummechanikai rendszerek numerikus vizsgálatát. Ha például a háromdimenziós hullámfüggvényt egy x, y,z-ben egyaránt 256 pontból állófelosztáson modellezzünk, a hullámfüggvény (duplapontos komplex) tárolásához 256 Megabyte tárolókapacitás szükséges - egy mai köznapi PC-ben általában több mint 1024 Megabyte memória található. Ha a számítást két dimenzióra korlátozzuk és/vagy kihasználjuk az adott rendszer szimmetriáit, akkor még kevesebb memória elegendő a számításokhoz.
Az MTA Műszaki Fizikai és Anyagtudományi Kutatóintézet Nanoszerkezetek Osztályán, belga kutatókkal együttműködésben kifejlesztett Web-Schrödinger egy olyan interaktív számítógépes szimuláció, amely szemléletessé teszi az időfüggő Schrödinger-egyenlet megoldását. A numerikus számítás maga egy alkalmazásszerveren fut, így a felhasználónak nem kell telepíteni semmit a saját számítógépén, egyszerű web-böngésző segítségével használhatja a programot ( http://www.nanotechnology.hu/online/web-schroedinger/index.html címen). A program interaktív voltából adódóan pedig a felhasználó betöltheti az előre elkészített példákat, és változtathat azok beállításain, továbbá készíthet teljesen új példákat, amelyek mentése szintén lehetséges. Ahhoz, hogy megértsük hogyan "kormányozhatja a hullámfüggvényt" a felhasználó a szimuláció során, kicsit részletesebben meg kell ismerkednünk a programmal.
Erwin Schrödinger 1926-ban [4] azzal a céllal alkotta meg a kvantummechanikai hullámcsomag fogalmát, hogy hidat építsen a klasszikus és a kvantummechanika között. A hullámcsomag egy térben lokalizált hullámfüggvény, azaz olyan kvantumállapotot ír le, amikor a részecske nagy valószínűséggel egy adott pont közelében található. A Schrödinger-egyenletből levezethető, hogy a hullámcsomag tömegközéppontja jó közelítéssel úgy mozog, mint egy klasszikus tömegpont, ha a potenciál lassan változik a hullámcsomag méretéhez képest. A hullámcsomag leggyakrabban alkalmazott formája a Gauss-hullámcsomag - a Web-Schrödinger program is ezt használja kezdőállapotként:
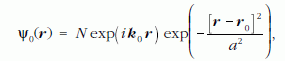
ahol k0 = (2π/λ)n a hullámcsomag hullámszámvektora, λ a de Broglie hullámhossz, a pedig a hullámcsomag szélessége - minél nagyobb a, annál szélesebb a hullámcsomag. Az n vektor a részecske haladási irányát adja meg, N pedig egy normálási faktor. A hullámszám a részecske lendületéből így számíthatóki: k0 = p0/ ħ, ħ= h/2π, ahol h a Planck-állandó. r0 adja meg a részecske helyét - a negatív kitevőjű exponenciális függvény miatt ezen a helyen maximális a Ψ hullámfüggvény abszolút értéke, r0-tól távolodva gyorsan csökken. Mivel ρ = |Ψ|2 adja a megtalálási valószínűségsűrűséget a hely függvényében, azonnal láthatjuk, hogy a Gauss-hullámcsomag valóban lokalizált állapotot ír le: a részecske megtalálási valószínűsége az r0 pontban a legnagyobb, attól távolodva rohamosan csökken - lásd a 2. ábrát!


|
Mint azt korábban részletesen leírtuk [5], a hullámcsomag- dinamikai módszerben egy adott potenciáltérben vizsgáljuk meg a hullámcsomag mozgását (szimulált szóráskísérlet). Ennek szemléltetése pedig kiemelkedő fontosságú, ugyanis a diákok nehezen tudják elképzelni, hogyan terjed egy elektron, mi történik, ha potenciálgáttal érintkezik, hogyan megy végbe a kölcsönhatás stb.
Elsőként a felhasználó a számolási doboz méretét, illetve annak felosztását tudja beállítani. Jellegzetes nanofizikai alkalmazásoknál a számolási doboz mérete néhány nanométer, a felosztást pedig úgy kell megadni, hogy a szimulációban előforduló de Broglie hullámokat jól mintavételezze. Elektronvolt nagyságrendű energiáknál ez - elektronra - 0,01-0,1 nm lépésközt jelent.
A második lépés a potenciálfüggvény megadása, voltaképpen ezzel határozzuk meg azt a fizikai rendszert, amelyet vizsgálni akarunk. A különböző potenciálokkal vagyunk tehát képesek különböző jelenségek szemléltetésére, mint például az alagutazás folyamata, a tiltott és megengedett sáv kristályokban, dobozba zárt részecske stb.
Háromfajta potenciál "építőkocka" közül választhatunk; a kör, a téglalap és a félsík, amelyeket tetszőleges módon és számban helyezhetünk el a számolási dobozban, természetesen értékeik megadásával, ezáltal széles alkalmazási spektrumot kínálva a felhasználónak. Az 1. ábrán, amely egy, a programból kimentett képernyőkép, láthatjuk, hogyan lehet bonyolult potenciálokat is egyszerűen felépíteni a programmal: ezen a képen egy szén nanocső pásztázó alagútmikroszkópos leképezésének szimulációjánál használt potenciált [5] mutatunk be. Az 1. ábrán az STM-tű - nanocső - hordozófelületnek a csőre merőleges keresztmetszetét láthatjuk: az alsó fekete félsík a hordozót, a középső gyűrű a nanocsövet (amely a Van der Waals potenciálon "lebeg" a hordozó fölött, körülbelül 0,335 nm távolságra), a fölső félsík a félkör alakú kiemelkedéssel az alagútmikroszkóp tűjét szimulálja. Az STM leképezésnek ezzel az egyszerű, geometriai modelljével számos kísérleti eredmény vált értelmezhetővé, amelyekről részletesen az alábbi cikkekben lehet olvasni [5-7].
A következő lépés a kezdeti hullámcsomag paramétereinek megadása. Itt tudja a felhasználó a hullámcsomag kezdeti helyét, kinetikus energiáját, szélességét és még egyéb, ehhez kapcsolódó adatokat beállítani.
Végül a már említett számolási lépésközt (δt) és a szimulált időtartamot adhatjuk meg. A számolás eredményét a program képek formájában jeleníti meg (results menüpont). A képeken a megtalálási valószínűségsűrűség, ρ(r, t) = |Ψ(r, t)|2 időfüggése látható.
Megismerkedvén lehetőségeinkkel, a cikk következő részében néhány példával szeretnénk bemutatni a program működését (ezek szintén megtalálhatóak a "példák" menüpont alatt).
A klasszikus fizika törvényei szerint egy E energiával rendelkező részecske nem tud behatolni V > E potenciállal rendelkező térrészbe, ez számára ugyanis tiltott tartomány. Ennek szemléletes példája a mély gödör alján lévő, abból kigurulni nem tudó labda esete. A kvantummechanika azonban mást mond: hullámtulajdonságából kifolyólag a részecskének van egy véges valószínűségű esélye arra, hogy áthaladjon az energiáját meghaladó"magasságú" potenciálfalon. Ezt a jelenséget nevezzük alagúteffektusnak, ennek nem egy megjelenési formájával találkozhatunk a természetben és a technikában, a radioaktív bomlástól a villanykapcsoló működéséig. A Web-Schrödingerrel most ezt a jelenséget szeretnénk bemutatni.
A beállítások kritériuma, hogy a potenciálfal magassága legyen nagyobb a hullámcsomag energiájánál. Ekkor az áthaladási valószínűség jó közelítéssel
T ~ e-2κd,
ahol κ paraméter a részecske tömegéből, energiájából, illetve a potenciál nagyságából számítható. Innen már látszik, hogy nem érdemes a potenciálfal szélességét túl nagyra választani, mert akkor az átjutás mértéke túlságosan csökkenhet, ezáltal a jelenség kevésbé szemléletes. A példában a potenciál értéke V = 7 eV, a kezdeti energia pedig E = 5 eV. A potenciál vastagsága d = 2 Ä. Ezekkel az értékekkel az átmeneti valószínűségre T = 0,17 értéket kapunk a fenti képletből, a visszaverődési valószínűség tehát R = 1-T = 0,83.A megtalálási valószínűségsűrűség időfejlődése a 2. ábrán látható. Mivel a kezdeti hullámcsomagnak egy -y ("lefelé") irányú lendületet adtunk, megfigyelhetjük, hogy időfejlődése során a -y irányba halad - amíg csak el nem éri a potenciálfalat. A további képek azt mutatják, ahogyan a hullámcsomag kölcsönhatásba lép a potenciálfallal, az utolsókép pedig a kölcsönhatás lezajlása utáni végállapotot ábrázolja. A teljes folyamat 2,32 fs = 2,32 · 10-15 s időt vesz igénybe. A vízszintes csíkokat a visszavert és beérkező hullámok interferenciája okozza. Látható hogy bár a részecske elég nagy eséllyel visszaverődik, mégis véges valószínűséggel átjuthat a potenciálfalon (szürke folt a potenciál túloldalán). Így tehát szemléletes képet sikerült alkotnunk az alagutazás folyamatáról.
Az ideális kristály a térben ismétlődő, azonos szerkezeti egységekből állórendszer . Ha egy hullám, amelynek hullámhossza összemérhető a kristály periodicitásával, kölcsönhatásba lép a kristállyal, akkor fellép a diffrakció jelensége. A diffrakció pedig erősen függ a hullámhossztól, ezáltal bizonyos hullámhosszú hullámok át tudnak hatolni a kristályon (megengedett sáv), míg mások visszaverődést szenvednek (tiltott sáv). Ha elektronok szóródnak, akkor ez a jelenség alakítja ki többek között az elektronok sávszerkezetét - ezen alapul a félvezető eszközök működése -, láthatófény szóródásánál pedig különböző színek megjelenését tapasztalhatjuk. Azokat a kristályokat, amelyek periodicitása a látható fény hullámhosszának nagyságrendjébe esik, fotonikus kristályoknak nevezzük, és bizonyos ásványoknál és élőlényeknél ez okozza a színpompás megjelenést. Ezzel részletesen az alábbi cikk foglalkozik [8].
A 3. ábrán bemutatott szimulációban a potenciálok megegyeznek, de a kezdeti állapotok energiái eltérőek, így szemléltetve a tiltott és megengedett sáv hatását. Láthatjuk, hogy a szimulációban a tiltott sáv esetén is van egy kis áthaladás és a megengedett sáv esetén is egy kis visszaverődés. Ez abból adódik, hogy a hullámcsomag nem egy energia-sajátállapot, azaz van egy bizonyos ΔE energiaszórása. Ezért a tiltott (megengedett) sávba eső hullámcsomag - kis valószínűséggel - áthaladhat (visszaverődhet) a kristály-potenciálon. A hullámcsomag ΔE energiaszórását természetesen tetszőleges mértékben csökkenthetjük, de ez csak azon az áron lehetséges, hogy a Δr térbeli kiterjedését megnöveljük (azaz egyre inkább közelítünk a síkhullám határesethez). Ám a hullámcsomag térbeli kiterjedésének növelése megnöveli a számolási doboz méretét is.
A szabad térbeli kvantummechanikai hullámcsomag - azaz, ha a részecske nem hat kölcsön semmi mással - alapvető tulajdonsága a szétfolyás, azaz a megtalálási valószínűség az idő előrehaladtával egyre nagyobb térrészre terjed ki. Megfelelő potenciál alkalmazásával azonban megfordíthatjuk ezt a folyamatot! Azt a jelenséget, amikor a kezdeti hullámcsomag időfejlődése folyamán újra kialakul a kezdeti állapot,
quantum revivalnek
(kvantumállapot újjászületés) nevezzük.
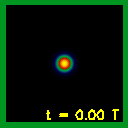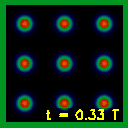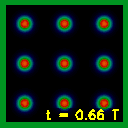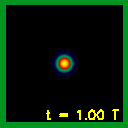
A kvantumállapot újjászületés bemutatásához a "dobozba zárt részecske" modellből indulunk ki, amelyben a hullámcsomag egy kétdimenziós potenciálgödörbe van lokalizálva. ρ(x,y; t ) időfejlődését láthatjuk a 4. ábrán, ahol a szimuláció teljes időtartama egy újjászületési periódus. Megfigyelhetjük, hogy a kezdeti hullámcsomag először elkezd szétfolyni, majd visszaverődik a potenciálfalról, interferencia-mintázatok alakulnak ki. A szimuláció végére rekonstruálódik a kezdeti állapot. Ám a közbenső időkben is bámulatosan érdekes jelenséget figyelhetünk meg, a többszörös (tört) újjászületéseket: a kezdeti hullámcsomag több példányban rekonstruálódik a potenciáldoboz különböző helyein. A többszörös újjászületések szimmetriaszerkezetét a V(r) potenciál szimmetriája szabja meg. Mivel a 4. ábrán a potenciál x és y irányban szimmetrikus, a kezdeti hullámcsomag x és y irányban is megismétlődik. Mint a hátsó boritón látható színes kép bemutatja, az újjászületés és a többszörös újjászületések bonyolult alakú hullámcsomagok esetén is bekövetkeznek. A 4. ábrán a fehér felel meg a nulla megtalálási valószínűségsűrűségnek, a fekete a legnagyobb megtalálási valószínűségsűrűségnek. Láthatjuk, ahogyan a hullámcsomag szétfolyik, úgy egyre szélesebb lesz, de egyre alacsonyabb lesz a csúcsa. Fizikailag ez azt jelenti, hogy a kezdeti, jól lokalizált állapotban a hullámcsomag az r0 hely (ami a 4. ábrán az origó) kis környezetében található nagy valószínűséggel, de később már nagyobb térrészre tejed ki. A többszörös rekonstrukciók esetén, ha a rekonstrukció n-szeres, a maximális megtalálási valószínűség 1/n2 arányban csökken a kiinduló állapothoz képest.
Természetesen az időfüggő Schrödinger-egyenlet megoldásán alapuló hullámcsomag-dinamikai szimulációkat nemcsak az oktatásban, hanem a kutatásban is eredményesen lehet használni. Ennek szemléltetésére a Web-Schrödinger példái közt szerepel még egy érdekes, a hétköznapi tudományból származó példa, amellyel az 1990-es években tanulmányoztuk a szén nanocsövek alagútmikroszkópos leképezését.
A kvantummechanika megértéséhez nagyon hatékony eszköz a számítógépes szimuláció, amellyel szemléletesen tudunk bemutatni különböző folyamatokat. A Web-Schrödinger egy ilyen szimulációs program, amely a szemléletesség mellett interaktív is. Ezáltal a diákok maguk készíthetnek példákat, modellezhetnek folyamatokat, amelyek segítségével mélyebben megérthetik a kvantummechanika jelenségvilágát.
A hullámcsomag-dinamikai szimulációk még a kvantummechanika filozófiai kérdéseit is segítenek megvilágítani - már az egyszerű alagútjelenség példája segítségével. Ugyanis a hullámcsomag, amíg nem éri el a potenciálgátat, egyenletesen halad és közben szétfolyik. A szétfolyás jelensége ellen még talán nem nagyon berzenkedik a klasszikus szemléletünk - annyi történik mindössze, hogy a részecske helyének "bizonytalansága" egyre nagyobb lesz. Ám az alagútjelenség lezajlása utáni végállapotban (2. ábra) azt láthatjuk, hogy a hullámcsomag két különállórészre oszlott, amelyek egyre távolodnak egymástól - azaz immár nem egy, hanem két hely van, amelynek környezetében nagy valószínűséggel megtalálhatóa részecske. Nevezzük ezeket A (a potenciálfal egyik oldalán) és B (a potenciálfal másik oldalán) helyeknek. Az idő múlásával a két rész-hullámcsomag bármilyen messzire távolodhat egymástól. De - mivel az egyrészecske hullámfüggvény valójában egyetlen tömegpont megtalálási valószínűségsűrűségét határozza meg - a részecske csak az A hely környezetében, vagy a B hely környezetében lehet, viszont az, hogy melyik helyen találjuk meg a részecskét, csak akkor derül ki, mikor megmérjük, hogy hol van. Ám amint megmérjük, hogy például az A oldalon van-e a részecske és azt találjuk, hogy ott van (illetve nincs), ekkor abban a szempillantásban meghatározottá válik, hogy a másik oldalon nincs (illetve van). Az A és B helyeken történő részecske helymeghatározás akkor is antikorrelációt fog mutatni, ha a két mérés között a t = d / c időnél rövidebb idő telik el, ahol d a két hely távolsága és c a vákuumbeli fénysebesség. Ezekről a kérdésekről lásd bővebben [10, 11] Geszti Tamás cikkeit!