Fizikai Szemle honlap |
Tartalomjegyzék |
Bokor Nándor
BME Fizika Tanszék
A speciális relativitáselméletnek a mindennapi szemléletünk számára meglepő következményeit sok gondolatkísérlet illusztrálja. Az egyik fogalmi újítás az időtartam abszolút voltának elvetése. Ehhez kapcsolódik az ikerparadoxon, amely többek között drámai megfogalmazásának – ikertestvérek életkora különbözhet, ha két találkozás között egymástól eltérő mozgást végeztek köszönheti népszerűségét.1 A különböző életpályájú ikrek eltérő öregedése, mint problémafelvetés azonnal felkelti a diákok érdeklődését. A paradoxon feloldása egyértelmű, matematikailag egyszerű, sok diák azonban joggal valami többet, szemléletesebbet vár a formulák felírásánál. Mi okozza (fizikailag) az eltérő öregedést? Ennek szemléletessé tételére az egyes fizikakönyvek már többféle magyarázattal próbálkoznak, ezek némelyike inkább a zavart fokozza az olvasóban, mintsem a megértést segíti. Sajnos a magyar mérnökhallgatók által legszélesebb körben használt egyetemi tankönyvek [1, 2] éppen ilyenek. A jelen cikknek kettős célja van: (1) rámutatni az ikerparadoxon-magyarázatok némelyikének félreérthetőségére; (2) bemutatni a paradoxonnak néhány olyan változatát, amelyekben a látszólagos ellentmondás még élesebben mutatkozik meg, és így végső soron mélyebbé tehetik a diákok számára az effektus megértését.
A magyar mérnökhallgatók által legszélesebb körben használt fizikatankönyv [1] így fogalmaz:
"Nem lehet az ikertestvérek közül bármelyiket mozgónak vagy nyugvónak tekinteni, és így a helyzetet szimmetrikusnak felfogni? Nem bizony! Mert az utazó testvérnek valamiképpen gyorsulnia kell, hogy a visszatéréshez megváltoztassa a sebességét, a gyorsulás pedig csak az utazó iker vonatkoztatási rendszerével kapcsolatos! A gyorsulás abszolút, nem pedig relatív dolog, ezért az esemény nem szimmetrikus."
Bár a könyv általában ügyel a pontos fogalmazásra, a diák a fenti részletet olvasva joggal érezheti úgy, hogy végre megértette az utazó iker lassabb öregedésének fizikai hátterét: az effektust valamiképp a gyorsulás okozza. Igaz, hogy a könyv siet a további magyarázatokkal: előbb lábjegyzetben említi, hogy "Kísérletileg (…) bebizonyították, hogy gyorsulások egészen a 1016 g értékig nem befolyásolják az órák járását. Csak a relatív sebességek teszik ezt." Majd később leszögezi: "A [fordulópontnál jelentkező] gyorsulás ugyan nem változtatja meg az órák járásának ütemét, de drámaian megváltoztatja az egyidejűség skáláját az S ' [az utazó iker nyugalmi rendszere] számára." Ezek a kiegészítések azonban – összevetve az elsőnek leírt magyarázattal – inkább csak zavarosabbá teszik, mintsem tisztáznák az olvasóban a kérdést, hogy a gyorsulásnak végül is van-e szerepe, vagy nincs.2
Még rosszabb a helyzet egy másik, széles körben alkalmazott tankönyvvel [2], amely egyszerűen így fogalmazza meg a két iker nem szimmetrikus mozgását:
"Speedo, az űrutazó kénytelen egy sor gyorsulási szakaszt átélni utazása alatt, hiszen be kell kapcsolnia a rakétáit, hogy előbb lelassítsa az űrhajóját, majd visszainduljon a Föld felé. Így sebessége nem lesz végig állandó, következésképpen nem inerciarendszerben utazik."
A könyv magyarázata itt gyakorlatilag abba is marad. Az olvasóban tehát ismét könnyen kialakul az a tévkép, hogy az effektusnak dinamikai oka van. Mintha az utazó iker attól öregedne kevésbé, hogy mozgása során erőlökéseknek van kitéve (és ez fiziológiai változásokat okoz a szervezetében).3
Az alapprobléma valószínűleg az, hogy a tankönyvek ikerparadoxon-változata szinte mindig egy gyorsulásmentesen (egyenes világvonal mentén) és egy gyorsulva (megtört vagy görbült világvonal mentén) mozgó iker életútját veti össze. Érthető persze ez a választás, hiszen ennek feltűnő aszimmetriáját (gyorsul – nem gyorsul) a diákok hamar átlátják. Másfelől éppen ez a feltűnő aszimmetria sodorja – még félrevezető magyarázatok nélkül is – szinte elkerülhetetlenül abba a képzetbe az olvasót, hogy a jelenségben a gyorsulás valamilyen fontos szerepet játszik.
Van olyan tankönyv [3], amely ugyan szintén a szokásos "gyorsul – nem gyorsul" ikerparadoxon-változatot tárgyalja, viszont – mivel tisztában van az így előálló csapdahelyzettel – hosszú, precíz magyarázattal tereli az olvasót a helyes fizikai kép felé:
"(…) szó sincs szimmetriáról: az ikerpár egyik tagja végig zavartalan sorsú, »szerencsétlen« testvére viszont mindenféle »zaklatásban« részesül. (…) Ugyanakkor arról sincs szó, hogy a kevésbé öregedésnek a »zaklatás« (gyorsulás) lenne az oka. A »szerencsétlen« sorsú testvérrel (…) csupán egyetlen egyszer történik valami »megrázó« (…), de nyilván nem ekkor és ettől »fiatalodott meg« hirtelen. Arról sincs szó, hogy az egyik testvér lassabban öregedne, mint a másik. (…) a két testvér nem különböző ütemben, hanem a téridő különböző irányában kezd öregedni. (…) Az eltérő időtartamoknak globális, téridő-geometriai oka van. (…) Az ikerparadoxon lényege tehát fizikai szempontból a következő: a téridő két eseménye között különböző világvonalakon mérve különböző (saját)időtartamok telnek el, méghozzá úgy, hogy a két eseményt egyenes világvonallal összekötve telik el a legtöbb idő."
A fenti magyarázat szemléletes és – a matematikai részletek elkerülése mellett is – teljesen precíz. Az eltérő öregedésért tehát nem a gyorsulás a felelős. Mégis, az olvasóban tovább motoszkálhat a kérdés: ha egyszer az ikrek sorsa feltűnő módon mégiscsak abban tér el, hogy az egyiket "zaklatják", a másikat "zavartalanul hagyják", akkor ez a különbség miben nyilvánul meg? Van-e a gyorsulásnak bármilyen szerepe az eltérő öregedéssel kapcsolatban, vagy teljesen kihagyható a diszkusszióból?
1912-ben von Laue a következőket írta [4]: a gyorsulás az effektusban egyáltalán nem játszhat szerepet, hiszen az oda-vissza utazó iker világvonalán "az egyenletes mozgás szakaszainak időtartamát tetszőlegesen nagyobbra választhatjuk, mint a gyorsulási szakaszokét". Ez a mondat azonban önmagában még nem meggyőző, hiszen – adott sebességváltozás mellett – minél kisebbre választjuk a gyorsulási szakasz időtartamát, annál nagyobbá válik a gyorsulás számértéke. Egyáltalán nem magától értetődő tehát, hogy ezzel a trükkel kiküszöböltük a gyorsulás szerepét a problémából.
Végül megemlítek egy olyan tankönyvet [5], amely az ikerparadoxon tömör megfogalmazását adja, úgy, hogy a gyorsulás szó használatát teljesen elkerüli:
"A trajektória t1 ≤ t ≤ t2 szakaszám eltelt sajátidőt az alábbi integrál adja meg:
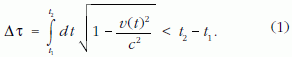
Ez a képlet írja le az ikerparadoxon néven ismert jelenséget. Tekintsünk két különböző tömegpontot, a-t és b-t, mindegyiket a saját órájával (…). Tegyük fel, hogy a t1 és a t2 (>t1) pillanatokban találkoznak egymással. (…) Ha [a fenti képlet] segítségével mindkettőre kiszámítjuk a két találkozás között eltelt sajátidőt, a va(t) és a vb(t) függvények különbözősége miatt általában két különböző Δτa, Δτb értéket kapunk."
Az (1) képlet azt is mutatja, hogy – összhangban von Laue fenti érvelésével – egy gyorsulási szakasz időtartamát nullához közelítve, bár a gyorsulás számértéke korlátlanul nő, a gyorsulási szakasz alatti sajátidő-járulék zérushoz tart:
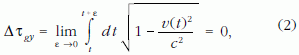
hiszen az integrálandó függvény korlátos (1-nél kisebb).
Az ár, amit a fenti pontos, kvantitatív tárgyalásért fizetünk, a szemléletes geometriai kép hiánya. Néhány példával és geometriai analógiával azonban még egyértelműbbé és érthetőbbé lehet tenni, hogy a gyorsulás az ikerparadoxonban valóban nem játszik szerepet. A legmeggyőzőbbek ebből a szempontból az olyan példák, amelyekben az ikrek (1) ugyanúgy gyorsulnak, mégis eltérően öregednek, vagy (2) különbözőképpen gyorsulnak, mégis ugyanúgy öregednek. Az alábbiakban ilyen ikerparadoxon-változatokat vizsgálok.
1. példa
Az alábbi változat szövege részletesen beszél az
ikrek által átélt gyorsulásokról. Mivel a gyorsulások
teljesen szimmetrikusak, a szövegből nehéz tetten
érni, mi vezethet az eltérő öregedéshez:
"Antal és Béla egy ikerpár, egy űrállomáson élnek. Mindketten beülnek űrhajójukba, és egyszerre elindulva a gyorsulással v sebességet érnek el. Hamarosan -a lassulással megállnak. Végül -a gyorsulással visszaindulnak (a végsebességük ezúttal -v), majd az űrállomás közelébe egyszerre érve a lassulással megállnak. Béla sokkal többet öregedett, mint Antal. Hogyan lehetséges ez?"
Az 1. ábra mutatja az egyszerű magyarázatot. A két iker világvonala feltűnően különbözik, így az eltérő öregedésben nincs semmi meglepő, holott az A1, A2, A3, A4, illetve a B1, B2, B3, B4 gyorsulási-lassulási szakaszok – így az ikreket ért erőlökések is – teljesen megegyeznek.
Az ikrek öregedését kiszámíthatjuk, ha az (1) képletet alkalmazzuk először az egyik, majd a másik világvonalra (a kvalitatív szemléltetéshez elég, ha – mint az 1. ábrán – a világvonalakra rajzolt pontokkal jelezzük az egyenlő sajátidő-tartamokat, például hónapokban mérve).
A feladat megszövegezésében a "csalást" nyilvánvalóan ott követtem el, hogy hallgattam arról: az ikrek visszafordulását eredményező fékezési, illetve gyorsulási manőverek az ikreknek nem ugyanannyi idős korában történtek.
2. példa
Lássunk egy másik, hasonló példát ([6] nyomán),
ahol a szöveg többször kitér arra is, hogy a gyorsulási
szakaszok mikor zajlottak (sajátidőben mérve), így
talán még nehezebb észrevenni, hol jelenik meg a
mozgás aszimmetriája:
"Két ikertestvér, Anna és Balázs, egy űrbázis közepén élnek. Az űrbázis mérete 1 fényév.4 20. születésnapjuk előtt egy nappal beülnek űrhajójukba, és elindulnak ellentétes irányban az űrbázis két széle felé: Anna balra indul, Balázs jobbra. A két űrhajó tökéletesen ugyanolyan, és a két iker vezetési stílusa is megegyezik, azaz a két mozgás tökéletesen szimmetrikus. Olyan gyorsan haladnak, hogy a 0,5-0,5 fényévnyi távolságot az űrbázis két széléig 1 nap alatt megteszik (saját órájukon mérve). Mindketten tehát 20. születésnapjukon érnek az űrbázis két szélére: Anna a bal, Balázs a jobb szélére. Még aznap elindulnak egy hosszú űrutazásra, mindketten jobbra. Ráérősen gyorsulnak fel; űrhajóik ismét pontosan ugyanúgy viselkednek, ezért Anna és Balázs mindig pontosan ugyanannyi idős korukban érnek el egy-egy adott sebességértéket. Éppen 30. születésnapjuk előtt egy nappal, amikor pontosan v = 0,999 c a sebességük, mindketten egy másik űrbázis mellé érnek. Ezen űrbázis sebessége is éppen 0,999 c, azaz hozzájuk képest nyugalomban van. Ki lehet szállni a száguldó űrhajóból, és egyszerűen lelépni a "száguldó" űrbázisra. Ezt mindketten meg is teszik még aznap, 30. születésnapjuk előtt egy nappal. Kiderül, hogy ez az űrbázis éppen olyan hosszú, hogy Anna a bal szélére, Balázs a jobb szélére lépett le. Az űrbázis közepén, félúton van egy étterem. Az ikerpár ott akar találkozni, hogy élményeiket megbeszéljék. El is indulnak egymás felé, mégpedig egyszerre (azaz olyan módon időzítve az indulást, hogy – azonos sebességű űrhajóikon egymás felé haladva – éppen egyszerre érjenek el az űrbázis közepén levő étteremhez). Annyira nagy sebességgel utaznak, hogy az út az űrbázis közepéig mindkettejük óráján csak 1-1 napot vesz igénybe. Anna tehát pontosan 30 éves, amikor az étteremhez egyszerre odaérnek. Meglepve látja, hogy egy sokkal idősebb férfi siet feléje: Balázs 52 éves!"
Az ikrek által átélt gyorsulási szakaszok, "rázkódások" ismét pontosan ugyanolyanok. Az egyetlen aszimmetria ott jelent meg, hogy jobbra indultak útnak, nem pedig balra (akkor Anna öregedett volna többet).
Az aszimmetriát mutatja, és a kvalitatív tárgyalásban segít a 2. ábra (K a kiindulási űrbázis nyugalmi rendszere, K' a végállomás nyugalmi rendszere, és A5 és B5 jelzi azt a két eseményt, amikor Anna, illetve Balázs egyszerre elindult az űrbázis közepén levő étteremhez). A feladat végigszámolását az olvasóra bízom.
3. példa
Mennyire tartozik hozzá egyáltalán a gyorsulás az
ikerparadoxonhoz? Lehet-e olyan példát konstruálni,
amikor egyik iker sem gyorsul, mégis eltérően öregednek?
Ez első látásra (legalábbis sík téridőben) képtelenségnek
tűnik, hiszen még ha az egyik iker gyorsulásmentesen
mozog (vagy helyben marad) is, a másiknak
el kell távolodnia, majd vissza kell fordulnia,
hogy ismét találkozhassanak. Ez a kifogás azonban az
alábbi ötlettel [7] kicselezhető: legyen a téridő továbbra
is sík (ahol a speciális relativitáselmélet uralkodik),
de zárt, ahogy a 3. ábra mutatja. A két iker – Aladár
és Béni – eltérő világvonalakon jut el a D eseményből
az E eseménybe, úgy hogy közben mindketten végig
állandó sebességgel mozognak.
Tekintsük Aladár nézőpontját, pontosabban megfogalmazva azt a globális inerciarendszert – nevezzük ezt KA -nak; (x, t) koordinátatengelyeit feltüntettem a 3. ábrán –, amelyben Aladár nyugalomban van. A jelenséget ebben az inerciarendszerben leírva Béni állandó v sebességgel jobbra halad, majd egyszercsak – mivel a téridő zárt – Aladár bal oldala felől visszajut a kiinduló pontba. Mivel inerciarendszerről van szó, alkalmazhatjuk az idődilatáció képletét, amelyből kiderül: az E-ben való találkozáskor Aladár idősebb, mint Béni.
A helyzet azonban most valóban szimmetrikusnak tűnik, hiszen egyik iker sem gyorsul! Ha Béni végig állandó sebességgel mozgott, akkor miért ne írhatnánk le ugyanígy a jelenséget abban az globális inerciarendszerben – nevezzük ezt KB-nek –, amelyben Béni van nyugalomban, és amelyből nézve Aladár "tesz egy kört", v sebességgel balra indulva? Világos, hogy KB-ben – mivel globális inerciarendszer – az idődilatáció képlete éppúgy alkalmazható, mint KA -ban. Csakhogy a képlet most az ellenkező eredményt adja: a találkozáskor Béni lesz idősebb, mint Aladár!
Hol az aszimmetria, amely a paradoxon feloldását lehetővé teszi? A válasz megtalálásához tekintsük a 4. ábrát, amelyre a KB globális inerciarendszer (x', t ') koordinátatengelyeit próbáltam berajzolni. A t '-tengely megegyezik a KB origójában nyugvó Béni világvonalával; az x'-tengely pedig ezzel szimmetrikusan helyezkedik el, ahol a szimmetriatengely egy D-ből jobbra indított fényjel világvonala. Több – egymással összefüggő – súlyos gond van azonban ezzel a konstrukcióval:
(1) Mint az ábrából is látható, a két koordinátatengely végtelen sokszor metszi egymást. Ez megengedhetetlen, hiszen azt jelentené, hogy téridőnek végtelen sok "origója van" (Béni az útja során periodikus időközönként a D indulási eseménybe jutna).
(2) KB-ben az órák fényjelekkel való szinkronizálása megoldhatatlan, mert – mint az ábrába könnyen berajzolható – ha Béni egyszerre küld jobbra és balra egy-egy fényjelet, a jobbra küldött fény előbb érkezik vissza hozzá, mint a balra küldött (aminek alapján – ha elfogadná nagy távolságokra is helyes hosszmérési eljárásnak ezt a módszert – Béni kénytelen lenne megállapítani, hogy zárt univerzumának kerülete balra mérve nagyobb, mint jobbra mérve!).
A hibát ott követtük el, hogy automatikusan feltételeztük: a 3. ábrán szereplő zárt téridő lefedhető olyan globális inerciarendszerrel (ezt neveztük KB -nek), amelyben Béni nyugalomban van. Most láthatjuk, hogy ilyen globális inerciarendszer nem létezhet. Ebben a téridőben – bár sík! – van egy abszolút, kitüntetett nyugalmi rendszer; KA az egyetlen Minkowski-koordinátarendszer, amely a teljes téridőt lefedheti. A KA -beli leírás helyes, a viszontlátáskor valóban Aladár lesz az öregebb. A KA-hoz képest – akár állandó sebességgel – mozgó megfigyelők nem tudják megkonstruálni a méterrudak és szinkronizált órák olyan rendszerét, amely a teljes téridőt lefedi, és amely az idődilatáció képletének tetszőlegesen nagy téridőtartományra kiterjedő használatát jogossá tehetné.5
Szoros geometriai analógia: egy hengerfelület geometriai értelemben sík ugyan – hiszen egy sík lap torzításmentesen felcsavarható hengerré –, mégis fontos különbség van egy kiterített sík lap és egy hengerfelület között. A kiterített sík lap végtelen sok, egymáshoz képest elforgatott, derékszögű koordinátarendszerrel globálisan lefedhető, ez azonban a hengerre már nem igaz. Ha egy négyzetrácsos papírlapot feltekerünk hengerré, a négyzetrácsok csak akkor adnak értelmes koordinátavonalakat a hengeren is, ha a sík lapot "egyenesen", a koordinátavonalak mentén tekertük fel.
Ebben a példában az ikerpár egyik tagja, Alfréd, nyugalomban van, a másikuk, Benedek viszont – Alfréd nyugalmi rendszeréből nézve – szinuszosan ide-oda mozog az x-tengely mentén [8], ahogy az 5. ábra mutatja. Az írásom elején idézett, félreérthető ikerparadoxon-magyarázatok olvasói ezúttal azt mondhatják: Benedek, mivel folytonosan erőlökéseknek van kitéve, kevésbé öregszik mint Alfréd. De valóban így van-e ez?
Benedek kitérése, sebessége és gyorsulása az idő függvényében (Alfréd inerciarendszeréből nézve):
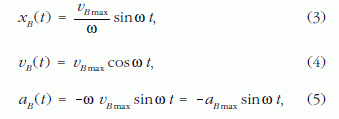
ahol ω Benedek mozgásának körfrekvenciája, vBmax és aBmax pedig sebességének, illetve gyorsulásának a csúcsértéke a nyugvó rendszerben mérve.6
Tegyük fel, hogy az F eseménytől a G eseményig Benedek n félperiódust tesz meg jobbra, illetve balra. Alfréd öregedése egyenlő a két esemény között eltelt koordinátaidő-tartammal:

míg Benedek öregedése az (1) idődilatációs képlet alapján írható fel:
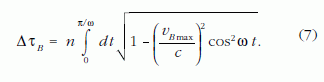
A (7) integrált θ = ωt új változóval átírva, és (7)-et (6)-tal elosztva a két testvér öregedésének arányára a következő összefüggést kapjuk:
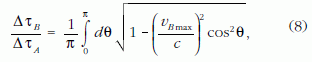
amely vBmax/c függvényében a 6. ábrán látható.
A (8) képlet és a 6. ábra legfontosabb tanulsága, hogy az öregedések aránya független az ω-tól. Ez viszont, mivel aBmax = ωvBmax, azt jelenti, hogy vBmax-ot kellően kicsinek választva a két testvér öregedésének arányát tetszőlegesen közel tarthatjuk 1-hez, miközben Bertalan maximális gyorsulását, ω-t alkalmasan nagyra állítva, tetszőlegesen naggyá tehetjük!
Összefoglalva: ebben a példában tehát a két iker közül az egyik nyugalomban van, a másik pedig tetszőlegesen nagy mértékben gyorsulhat, mégis – legalábbis határesetben – azonos mértékben öregednek.
Az összes eddigi példa illusztrálja, hogy nem az átélt gyorsulás (vagy annak hiánya) az ikerparadoxon megoldásának kulcsa.
Tekintsünk ugyanakkor egy olyan helyzetet, amikor az indulási és érkezési események között nem csak két iker, hanem tetszőegesen nagyszámú megfigyelő utazik. Az ilyen probléma tárgyalásában a gyorsulás fogalma ismét felbukkanni látszik. A maximális öregedés elvének [9] szokásos megfogalmazása szerint ugyanis a két esemény között azon utazó számára telik el a legtöbb sajátidő, aki szabadon, gyorsulásmentesen mozgott.
Hogyan illik bele ez az eddig elmondottakba? Van-e szerepe legalább a legtöbbet öregedő iker kiválasztásában a gyorsulásnak (illetve a hiányának)? A fenti 5. és 6. ábra példája azt mutatja, hogy végső soron nincs. Ebben a körmönfont példában láthattuk, hogy nem csak a gyorsulásmentesen mozgó Alfréd, hanem a szinuszosan ide-oda mozgó, gyorsulásokat átélő Benedek is a lehető legtöbbet öregedik az F és G események között. Világvonalukat végső soron nem a gyorsulás megléte vagy hiánya teszi különlegessé, hanem az, hogy mindkettő egyenes (illetve Benedek esetében tetszőleges pontossággal közelíti azt).
Jól megvilágítja ezt az alábbi geometriai analógia:
1. Sík papírlap 7
Két pont között húzunk egy vonalat, majd ugyanazt
a két pontot egy másik vonallal is összekötjük. Az
egyik vonal rövidebbre sikerült. Melyik?
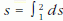 összhossza kisebb." Ez
persze triviális válasz. Szerencsére azonban alkothatunk
egy olyan geometriai fogalmat, az egyenesség fogalmát,
amely – ha megfelelőképpen definiáljuk – szemléletesebb
választ is lehetővé tesz a kérdésre. Mi legyen
az egyenesség mértékének definíciója? Milyen
értelemben nevezzük egyenesebbnek egy vonalat egy
másiknál? Az biztos, hogy nem elég, ha egy vonal
egyenesnek néz ki (gondoljunk például arra a nevezetes
álbizonyításra, amely egy derékszögű háromszög
befogóit – feltördelve, de a hosszukat változatlanul
hagyva – levetíti az átfogóra, és mivel a rengeteg
darabra feltördelt vonal láthatóan "rásimul" az átfogóra,
kijelenti, hogy a+b = c).
összhossza kisebb." Ez
persze triviális válasz. Szerencsére azonban alkothatunk
egy olyan geometriai fogalmat, az egyenesség fogalmát,
amely – ha megfelelőképpen definiáljuk – szemléletesebb
választ is lehetővé tesz a kérdésre. Mi legyen
az egyenesség mértékének definíciója? Milyen
értelemben nevezzük egyenesebbnek egy vonalat egy
másiknál? Az biztos, hogy nem elég, ha egy vonal
egyenesnek néz ki (gondoljunk például arra a nevezetes
álbizonyításra, amely egy derékszögű háromszög
befogóit – feltördelve, de a hosszukat változatlanul
hagyva – levetíti az átfogóra, és mivel a rengeteg
darabra feltördelt vonal láthatóan "rásimul" az átfogóra,
kijelenti, hogy a+b = c).
Az egyenesség mértékének definíciója: két pont között az a vonal az egyenesebb, amelyre s kisebb szám.
A sík lefedhető globális Descartes-koordinátarendszerrel ("négyzethálóval"). Ilyen koordinátarendszert használva, az adott görbe y (x) alakját ismerve a következő képlet alkalmazható s kiszámítására:
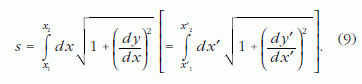
A (9) képlet szögletes zárójeles kiegészítése arra hívja fel a figyelmet, hogy a kiszámított számérték koordinátarendszer-független. Pontosabban: ha a sík adott tartományát – amely elég nagy ahhoz, hogy a végpontokat és a két görbét magában foglalja – az (x, y) négyzethálóhoz képest elforgatott (x', y ') négyzethálóval fedjük le, az új koordinátarendszerben felírva az adott görbe y '(x') alakját, ismét pontosan ugyanolyan alakú képlet alkalmazható s kiszámítására. Az, hogy globális Descartes-koordinátarendszerek használhatók, amelyekben a koordinátakülönbségek (9)-es képletbeli kombinációja invariáns (ugyanaz a vesszőtlen és a vesszős koordinátarendszerben), az euklideszi sík legfontosabb sajátossága.8
2. Sík téridő9
Két esemény között halad két részecske, két különböző
világvonalon. Az egyik részecske öregedése
nagyobb. Melyiké?
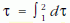 sajátidőtartam nagyobb." Szerencsére itt is
alkalmazhatjuk a világvonal egyenességének szemléletes
geometriai fogalmát, feltéve hogy itt is gondosan
definiáljuk ezt a fogalmat. Milyen értelemben
tekintsünk egyenesebbnek egy világvonalat egy másiknál?
Az ismét nem elég, ha egy világvonal egyenesnek
néz ki. (Gondoljunk például egy olyan, az 5.
ábrához hasonló esetre, amikor a szinuszos mozgás
helyett egy fénysugár pattog jobbra-balra az origó
közelében, és így jut el az F eseményből a G eseménybe.
A fordulók számának növelésével a fény
töredezett világvonala tetszőlegesen "belesimítható"
a t-tengelybe. A fénysugár számára eltelt sajátidő – a
világvonal hossza – mégis drasztikusan különbözik
Alfréd és Benedek világvonalainak hosszától: az utóbbiak
megegyeznek, és a leghosszabb sajátidőt képviselik,
a fény sajátideje viszont a lehető legrövidebb,
tudniillik zérus.)
sajátidőtartam nagyobb." Szerencsére itt is
alkalmazhatjuk a világvonal egyenességének szemléletes
geometriai fogalmát, feltéve hogy itt is gondosan
definiáljuk ezt a fogalmat. Milyen értelemben
tekintsünk egyenesebbnek egy világvonalat egy másiknál?
Az ismét nem elég, ha egy világvonal egyenesnek
néz ki. (Gondoljunk például egy olyan, az 5.
ábrához hasonló esetre, amikor a szinuszos mozgás
helyett egy fénysugár pattog jobbra-balra az origó
közelében, és így jut el az F eseményből a G eseménybe.
A fordulók számának növelésével a fény
töredezett világvonala tetszőlegesen "belesimítható"
a t-tengelybe. A fénysugár számára eltelt sajátidő – a
világvonal hossza – mégis drasztikusan különbözik
Alfréd és Benedek világvonalainak hosszától: az utóbbiak
megegyeznek, és a leghosszabb sajátidőt képviselik,
a fény sajátideje viszont a lehető legrövidebb,
tudniillik zérus.)
Az egyenesség mértékének definíciója: két esemény között az a világvonal az egyenesebb, amelyre τ nagyobb szám.
A sík téridő lefedhető globális Minkowski-koordinátarendszerrel. Ilyen koordinátarendszert használva, az adott világvonal x(t) alakját ismerve a következő képlet alkalmazhatót τ kiszámítására:
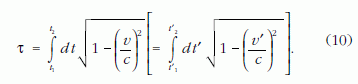
A (10) képlet szögletes zárójeles kiegészítése arra hívja fel a figyelmet, hogy a kiszámított számérték koordinátarendszer-független. Pontosabban: ha a téridő adott tartományát – amely elég nagy ahhoz, hogy a két szélső eseményt és a két világvonalat magában foglalja – az (x, t) inerciarendszerhez képest mozgó (x', t') inerciarendszerben írjuk le, az új koordinátarendszerben felírva az adott világvonal x'(t') alakját, ismét pontosan ugyanolyan alakú képlet alkalmazható τ kiszámítására. Az, hogy globális Minkowski-koordinátarendszerek használhatók, amelyekben a (10)-es képletalak invariáns – ugyanaz a vesszőtlen és a vesszős koordinátarendszerben – a sík téridő legfontosabb (tisztán geometriai) sajátossága.10
_______________________