Fizikai Szemle honlap |
Tartalomjegyzék |
Schronk Edina, BME mechatronikai mérnök szakos hallgató
Daróczi Csaba Sándor, MTA TTK MFA
A téma eredete az MTA MFA által 2011-ben kiírt NanoDemo pályázatig nyúlik vissza, amelyben nanojelenségek látványos bemutatására alkalmas kísérleti elképzeléseket kerestek, hogy a legjobbak profi megvalósítás után a Csodák Palotája gondozása alatt országot járó Nanobusz révén bárhol bemutathatók legyenek – ilyen módon is népszerűsítve a nanojelenségeket és -tudományt, főleg a középiskolás fiatalok, de akár az egész lakosság körében is. E pályázatra született a Nanovastagságú buborékhártya-kondenzátor címu terv is (Schronk Edina). Ez utólag nehezebben megvalósíthatónak bizonyult, mint eleinte hittük. Szerencsére a felmerült nehézségek "kerülgetése" nem volt terméketlen, egyéb érdekes kísérleti lehetőségek is adódtak, eleinte nem is gondoltuk volna. Így, bár a végcélt még nem értük el, szívesen adunk ízelítőt az eddigiekből, hátha mások is kedvet kapnak az effajta kísérletezéshez (például fizikakémia szakkörön).
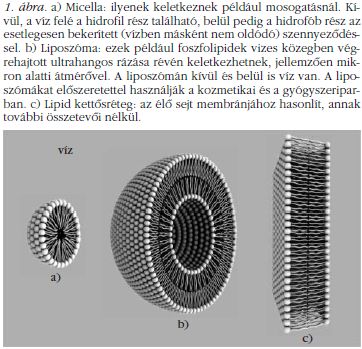
A NanoDemo pályázathoz kerestünk valamit, ami legalább az egyik dimenziójában nagyon kicsi, mint például a szappanbuborékok fala, amely köztudottan vékony. (Többnyire mikron körüli, azaz a látható fény hullámhossz-tartományába esik, innen a színjátszós hajlama.) De nem kimondottan a szappanbuborékokkal szerettünk volna foglalkozni, mert azokat már mindenki ismeri, noha szerkezetük nem olyan magától értetődő: a faluk valójában 3 rétegű, belül víz, kifelé szappanhártyával határolva, mégpedig úgy, hogy a "szappanmolekulák" hidrofil része a belső víz felé áll, a hidrofób pedig a külső levegő felé. A víz e szappanos "ruhán" keresztül nem párolog olyan gyorsan, mint egyébként, de azért így is egyre fogy, és ha mennyisége egy kritikus szint alá csökken, a hártya átszakad, a buborék pedig elpukkan. A rétegsorrend mindenesetre a következő: szigetelő-vezető-szigetelő (tudniillik a nem teljesen tiszta víz elég jól vezet). Ha a sorrend valamiképp vezető-szigetelő-vezető lenne, akkor pont egy elektromos kondenzátort kapnánk!
A levegőben erre nem találtunk létező példát, de azután leesett a tantusz: ha a kiindulási közeg nem levegő, hanem víz, akkor megfordulnak a dolgok, vagyis ha a vízben hozzuk létre a szappanbuborék megfelelőjét, akkor a szappanmolekulák hidrofil része kifelé (az elektromosan vezető víz felé) fog állni, a hidrofób pedig a réteg belseje felé, ahol mondjuk egy elég jó szigetelő, olaj lehetne. Egy ilyen sajátságos víz alatti buborék fala már kondenzátorként viselkedhetne, és ezért kapacitását megmérve vastagságára is következtethetnénk.
Azután persze rájöttünk, hogy a természet (közelebbről az élővilág) e téren (is) jóval előttünk jár, ugyanis az élő sejtek hártyája valóban hasonló felépítésű: a sejtek belseje (citoplazma) és a külvilág is elektromosan elég jól vezető vizes közeg (elektrolitként hasonlít az ősi óceánok összetételére), míg a hártya belseje lipid-fehérje komplexum, viszonylag jó szigetelő képességgel. Éppen ezért lehetséges az is, hogy a sejtek külseje és belseje között elektromospotenciál-különbség legyen (pár száz mV), aminek igen nagy jelentősége van például izom- és idegsejtek esetében. Mindez megerősített minket abban, hogy az általunk létrehozni kívánt hártya is megalkotható/elkészíthető valahogy, és kondenzátorként is vizsgálható, csak felülete legyen elég nagy, stabil és viszonylag könnyen reprodukálható (ez utóbbival akadtak gondjaink, de ne vágjunk a dolgok elébe). A főbb lehetőségek áttekintéséhez lássuk az 1. ábrát.
Célunk az volt, hogy vizes közegben létrehozzunk a liposzómákhoz hasonló, csak éppen makroszkopikus méretű "buborékokat" (avagy cseppeket), a vízhez szappanos és olajos természetű anyagokat adva, a szappanbuborékok fújásához hasonló geometriai elrendezésben, gondoskodva még elektródákról is, amelyek közül az egyik a buborék belsejével, a másik a külsejével áll galvanikus kapcsolatban. Így az elektródák között mérhető kapacitásban benne lenne a buborékot határoló szigetelőhártya kapacitása is, amit pedig egy alkalmasan választott frekvenciájú, négyszögjel alakú töltő-kisütő áram segítségével mérhetünk, ha egy oszcilloszkópon megfigyeljük a kondenzátorunkon folyamatosan változó feszültséget.
A buborékok létrehozásához a 2. ábrán látható konstrukciót ötlöttük ki. Veszünk egy felemás hosszúságú U alakú üvegcsövet, amely rögzítve van egy vizes kád (akvárium) belső falához. Az U-cső alacsonyabb szárának nyílásánál próbáljuk majd létrehozni a buborékot. Ehhez (a) a kádat feltöltjük vízzel eddig a szintig, a cső belsejébe pedig beengedjük azt a folyadékkeveréket, amelyben benne vannak a hártyaképző anyagok is, vagyis némi mosogatószer és olajos szennyeződés, valamint egy kevéske tinta, hogy jól meg tudjuk figyelni a kétféle víz mozgását. Ezután (b) a kádba óvatosan további vizet eresztünk, ezért a tintás víz szintje az alacsonyabb szárban csökkenni, a másikban meg emelkedni fog (közlekedő edények). A következő (c) lépésben az U-cső magasabb szárán át annyi plusz tintás folyadékot engedünk be, hogy a tintás víz az alacsonyabb szár tetejéig emelkedjen. Ezután már élesben mennek a dolgok, (d) mert nagyon óvatosan kell tovább folytatni a tintás víz beengedését (egyszerre csak egy csepp tört részét engedhetjük be).
A kétféle víz találkozásának határán, vagyis az alacsonyabbik szár tetején bizonyos valószínűséggel kialakul egy, a cső teljes keresztmetszetén átívelő hártya. Ha ez a hártya elég erős volna, akkor kis buborékot is "fújhatnánk" – de az igazat megvallva, már egy félbuborék kidudorodásának is nagyon lehet örülni. Sokféle dologgal kísérleteztünk, hogy stabil félbuborékot hozzunk létre, de eddig még nem jártunk sikerrel. Ezért ezen a ponton módosításra szántuk el magunkat. A részletezés előtt viszont még megjegyeznénk, hogy a könnyebb áttekinthetőség kedvéért a 2. ábrán nincsenek feltüntetve az elvezető elektródák. Az egyik elektróda az U-cső alacsonyabbik szára körül van gyűrű alakban kívül, míg a másik belül. Utóbbihoz a hozzávezetés az U-cső belsejében halad, majd a magasabb száron át lép ki. Ezért, ha létrejött a szigetelő hártya, akkor a két elektróda galvanikusan már nem lesz kapcsolatban. Amíg viszont nincs meg a hártya, addig a két elektróda a vízen keresztül "rövidre záródik".
Minthogy a tervezett formában nem tudtunk elég stabil buborékhártyákat létrehozni, biztosabb módszert kerestünk. Ennek lényege, hogy egy gyorsan párolgó oldószerrel készített oldatot cseppentünk a víz felszínére, ahol az oldószer elpárolgása után visszamarad egy nagyon vékony hártya. Hogy pontosan milyen vékony, az függ az oldott anyagtól, az oldószertől és a csepp nagyságától is. Alkalmasak különféle híg folyékony ragasztók (pálmát és ciano-akrilát alapú polimerizációsakat is beleértve), körömlakkok (hölgyek előnyben ), de a legjobbnak eddig a körömlakklemosóban oldott, celluloid alapú pingponglabda bizonyult. A hártya kialakulása gyakorlatilag másodpercek alatt lezajlik, és ha nem is mindig színjátszós (ez a vastagság függvénye), kissé oldalról nézve – a víz felületi mozgásának megváltozása miatt – jól látható. Az így létrehozott hártyát már csak a helyére kell mozgatni, hogy meg tudjuk mérni. A vízből kivenni általában lehetetlen, ahhoz ugyanis nem elég erős. De egy vékony dróthurokkal minden további nélkül oda lehet vontatni az U-cső alacsonyabb szárának tetejéhez, majd felülről óvatosan nedvesítve (permetezéssel és cseppentéssel) a víz alá süllyeszteni. Az ellenállás megnövekedése, illetve a kapacitás megjelenése mutatja, ha akciónk sikeres volt.
Amíg nem állt rendelkezésünkre elfogadhatóan vékony hártya, addig azt sem tudtuk megállapítani, hogy egyáltalán elég jó-e mérési összeállításunk, már ezért is szerencsés döntés volt a hártya előállításának módosítása. Kiderült, hogy az U alakú cső szárában haladó belső elektródát érdemes a víz helyett levegővel körülvenni, hogy a szórt kapacitás minél kisebb legyen. Felesleges a tintás folyadéknak az U-cső teljes keresztmetszetében haladnia, mert elég hozzá egy vékonyka tefloncső is, és akkor az U-csőben – leszámítva az alacsonyabb szárának tetejéhez közeli 1-2 cm-t, ahol a belső elektróda található – szinte végig levegő maradhat. Az is kiderült, hogy az oszcilloszkóp bemenő kapacitása (33 pF), valamint a hozzá vezető koaxiális kábel további kapacitása (50 pF) már akkora, hogy képes meghamisítani a kisebb kapacitások (vastagabb rétegek) mérését. Ezért egy RC-tagokból álló előosztót használunk, hogy a mérést megzavaró kapacitás csak mintegy 12 pF legyen. Végül sokat tudtunk javítani az érzékenységen azzal, hogy a vizsgált hártyakondenzátort nem önmagában mérjük, hanem egy ellenfázisú hídban, összehasonlítva a hártya nélküli esetnek megfelelő kapacitással és ellenállással.
A mérés és kiértékelése alapelvét egyszerűsített formában láthatjuk a 3. ábrán: a 0,2–200 kHz frekvenciatartományban választunk egy olyan frekvenciát, ahol jól látható a vizsgált kondenzátor hatása, vagyis amikor a bejövő négyszög alakú feszültség egy R1 ellenálláson át tölti és süti ki a hártyát (a Cx kondenzátort), akkor a feszültség alakja jellegzetesen torzul. Ilyenkor a feszültség a maximális értéke 63%-át (pontosabban 1/e -ed részét) éppen R1Cx idő alatt (a τ időállandó alatt) éri el. Ezért oszcilloszkópon megmérve a τ időt, az R1 ellenállás ismeretében egy egyszeru osztással kapjuk a kérdéses kapacitást: Cx - τ/R1.
(Felvetődhet a kérdés: miért nem használunk gyári kapacitásmérőt? Nos azért, mert akkor a mérő frekvenciát és annak nagyságát nem tudnánk hozzáigazítani a mérésünkhöz, továbbá mert az ilyen műszereket ismeretlen mértékben – de sokszor nagyon – zavarják az olyan körülmények, mint esetünkben a viszonylag alacsony értékű párhuzamos ohmos ellenállások, továbbá egyenáramok és -feszültségek is jelen lehetnek.)
Mérésünk alapötletének megértéséhez a 3. ábra elegendő. Aki hozzánk hasonlóan kísérletezni is szeretne, annak hasznos lehet a 4. ábrán látható teljesebb elektronikai rajz. Különösebb részletezés nélkül: a C4R7, C5R8 és R9 képezik azt az osztót, amely hivatott az oszcilloszkóp és a koaxiális kábel bemenő kapacitását és ellenállását (C6 és R10) kompenzálni a bejövő híd fölső és alsó ágáról is. Rx a víz hozzávezetési ellenállása, Cx a hártya ismeretlen kapacitása. C1, C2, R5, R6 és C3 a víz és az elektródák hártya nélküli dielektromos viselkedését modellező komplexum a használt (200 Hz – 200 kHz) frekvenciatartományban. R1, R2, R3, R4, D1, D2, D3 és D4 az esetleg tökéletlen alakú négyszögjel szimmetrizálását végzik limitálással.
A vizsgált Cx kondenzátor létrehozása/beiktatása előtt – helyén ilyenkor rövidzár van – az R5 potenciométerrel úgy minimalizáljuk a jelet, hogy szinte csak egy egyenes vonal maradjon. Ekkor R5 értéke csaknem azonossá válik a víz hozzávezetési ellenállásával, ebből megtudjuk Rx értékét. A szigetelő hártya képződésével a híd egyensúlya felborul, és az oszcilloszkópon megjelenik a jellegzetesen torzult négyszögjel alak. Számunkra a frekvencia pontos értéke közömbös, mint ahogy a jel abszolút nagysága is. Egyedül az érdekes, hogy maximális amplitúdója 63%-át mennyi idő alatt éri el (időállandó), ezt kell megállapítanunk.
Mondják, hogy "akinek a kezében kalapács van, az
hajlamos mindent szögnek nézni" 
. Hát mi meg úgy
jártunk, hogy amióta működik módszerünk, azóta
hajlamosakká váltunk mindent kondenzátornak nézni .
Rövid idő alatt sokféle anyagot kipróbáltunk. Az
eredményeket egy Excel-táblázattal értékeljük ki,
benne az érvényes fizikai összefüggésekkel (1. táblázat).
Az egyes hártyák vastagságnak megállapításához
a mért kapacitáson túl ismernünk kell a szigetelő
réteg relatív dielektromos állandóját. Ez nem mindig
egyértelmű – például a hőmérséklet vagy a víztartalom
is jelentősen befolyásolhatja –, ezért az irodalomban
fellelhető minimális és maximális értékkel is elvégeztük
a számításokat.
Az eredetileg megfigyelni kívánt hártyák mellett
kíváncsiak lettünk fémeken lévő lakk, zománc, illetve
festékrétegekre is, de ugyanígy megnéztünk polietilén
fóliát, csillámlemezt, üveget stb. Ezeket is kényelmesen
tudjuk mérni, csupán rá kellett szerelnünk az
U-cső alacsonyabb szárának tetejére egy lapos és
sima, kiszélesedő műanyag nyakat, amire a fémlemezeket könnyen ráfektethetjük
(5. ábra). Találtunk egy
szépen eloxált alumínium lemezdarabot is, ami ráirányította
figyelmünket a különféle fémek felületi
(többnyire vékony) oxidrétegeire. Most már gond
nélkül észleljük a nem eloxált alumíniumlemez vékonyabb
és ezért nagyobb kapacitású, ugyanakkor kényesebb
oxidját is, de látjuk a vörösréz és a sárgaréz
lemezekét, sőt a félvezető mikrotechnológiai osztálytól
kapott szilíciumlemez felületi oxid- és nitridrétegeit
is (elő és hátoldalit!). Érdekes módon ezen oxidok
vastagsága sokszor tényleg a nanotartományba
esik (1. táblázat ), szóval ilyen szempontból is mondhatjuk,
sikerült eredményt elérnünk. Terveink szerint
majd visszatérünk az eredeti feladatra, de az már egy
másik történet lesz .
A táblázat mérési eredményeinek első csoportjában olyan szigetelő anyagok vannak felsorolva (vastag celofántól a szilikongumiig), amelyek vastagságát tolómérővel közvetlenül is meg tudtuk határozni (bal szélső számoszlop), így ez referenciául szolgálhat a módszer pontosságára. A mért kapacitásokból számolt maximális vastagságok (jobb oldali oszlop) elég jól közelítik a tolómérővel kapottakat. Nagyobb eltérés (több mint egy 2-es faktor) csupán a gumikesztyűnél adódott, de annak vastagsága változékonyabb is. Az ilyen, viszonylag vastag anyagok kis kapacitásokra vezetnek (tipikusan 100 pF alattira), ami nagy működési frekvenciát tesz szükségessé (100–200 kHz). A kompenzáló hálózat hibája itt már nem hanyagolható el, ezért τ értékét korrigálnunk kell a "végtelen vastag" szigetelőnél kapott értékkel, ami esetünkben 0,8 ?s. A mérési összeállításról készült fotómontázs az 5. ábrán látható.
A következő csoportban különféle fémlemezek mérési eredményeit láthatjuk (alumínium, réz, ón). A fémek esetében azért alakul ki kapacitás, mert felületükön – többnyire – egy nagyon vékony oxidréteg képződik, amely dielektrikumként viselkedik. A rétegvastagságokat itt alternatív módszerrel nem tudtuk megmérni, de a kapott eredmények hihetőek. Megjegyzendő, hogy amikor egy nagyobbacska fémlemezt mérési pozícióba viszünk (azaz ráhelyezünk az U-cső alacsonyabbik szárának tetejére a víz alatt), akkor egyszerre több kondenzátor is létrejön: először az általunk vizsgálni kívánt kondenzátor közvetlenül a cső nyílásával szemben (vagyis a belső víz felé), másrészt mindenhol máshol a fémlemez felületén a külső víz felé. Ha elég nagy a lemez, akkor e másodlagos kondenzátor kapacitása sokkal nagyobb, és mert sorba kapcsolt kapacitásokról van szó, az eredő kapacitást a minket érdeklő kisebb kapacitás határozza majd meg. Ezért a mérési eredmények legfeljebb csak pár százalékkal mutatnak majd kisebb kapacitást, és ezzel együtt nagyobb rétegvastagságot. De ha olyan kicsi lemezt készítünk, amely éppen csak le tudja fedni az U-cső nyílását, akkor annak túloldalán ugyanakkora lesz a másik kapacitás (azonos minőségű lemezoldalakat feltételezve), és ezért a módszerünk által mutatott kapacitás feleződni fog, a rétegvastagság meg duplázódni (lásd a táblázatban a nagy és a kicsi eloxált alumíniumlemezek összehasonlítását.)
A harmadik csoportban 0,6 mm vastag szilícium félvezető szeletek vannak, ismert vastagságú fedő szilícium-oxiddal (100 nm), illetve -nitriddel (300 nm). A szeletek belsejében a fajlagos elektromos ellenállás 64 kΩcm körüli, ám a fényes oldalon közvetlenül a fedő réteg alatt kialakítottak bennük egy nagyságrendileg mikron vastagságú, de elektromosan elég jól vezető szennyezett réteget is (az oxidos mintánál n-típusút, 5 Ωcm fajlagos ellenállással, a nitrides mintánál pedig p-típusút, 15 Ωcm fajlagos ellenállással). Ez érdekes következményekre vezet a fémeknél megismert másodlagos kapacitások szempontjából. Itt nem részletezett számításokkal kimutatható, hogy az U-cső nyílásával szemben a Si-szelet túloldalán egy körülbelül ugyanakkora effektív kapacitás érvényesül, mint a mérni kívánt elsődleges kapacitás, miközben oldalirányban a nagy felület a nagy hozzávezetési ellenállás miatt már nem tud jelentős többlet-kapacitást adni. Ugyanakkor a szennyezett rétegek valamennyivel csökkentik az ellenállást, elsősorban az oxidos mintánál (az n-típusú réteg kisebb ellenállása miatt). Végeredményben a nitrides mintánál a 2 darab sorba kötött kapacitás miatt dupla rétegvastagságot mérünk, az oxidos mintánál pedig a mért vastagság a szerint duplázódik vagy sem, hogy a szennyezett, vagy a másik oldalról mérünk-e.
A negyedik csoportba tettük a celluloid hártyákra kapott 2 mérési eredményünket. (Vastagabb és vékonyabb hártyákat is tudunk készíteni.) A vastagság megállapítását itt az az effektus zavarja, hogy a celluloid a víz egy részét magába szívhatja, megváltoztatva a dielektromos állandóját. Ezért az ilyen jellegű anyagoknál mindenképpen szükségesek lesznek kiegészítő vizsgálatok.
Bár módszerünk már így is használható, távolról sem tökéletes. Például, ha a vizsgált kondenzátor töltéséhez áramgenerátort használnánk és nem egyszerű ellenállást, akkor nem kellene a jel alakját az oszcilloszkópon figyelgetni, mert az mindig háromszög lenne, így elég volna az amplitúdóját mérni, amihez még oszcilloszkóp sem feltétlenül szükséges, ami az érzékenységet és a pontosságot is javíthatná. Ugyanakkor egy széles frekvenciatartományban jól működő szimmetrikus áramgenerátor nem mindenkinél kallódik a polcon…
Egy ilyen jellegű projekt fő előnye (érdekessége mellett), hogy benne természetes módon találkoznak a mérnöki, fizikai, matematikai, mechanikai, elektromosságtani, kémiai és biológiai ismeretek – az ember szinte a bőrén érezheti, hogy a természettudományok elméletei hol és hogyan hasznosulnak a gyakorlatban. Megfigyelhetjük például, miként változik a felületi oxid vastagsága a vizes elektrolitban, vagy a hőmérséklet hogyan befolyásolja e nagyon vékony szigetelő hártyák (például szerves anyagok) vastagságát és víztartalmát. Minden megválaszolt kérdésre adódik egy sor újabb érdekes kérdés, szinte bármelyik tudományból. Különösen Magyarországon lehet fontos ez a felismerés, mert a PISA-felmérések szerint a magyar iskolarendszer jellemzője, hogy sokszor a gyakorlatban nem eléggé jól hasznosítható, passzív ismeretekkel bocsátja útjukra a diákokat [1–3].
Szerencsére az én középiskolámra ez nem jellemző, köszönettel tartozom matematikatanáraimnak, Rózsáné Motkó Editnek és Jarábik Bélának (aki egyben fizikatanárom is volt), Inczeffyné Vigh Gyöngyi Noémi fizika-, valamint Grószné Kiss Annamária biológia-tanárnőnek az elméleti és gyakorlati ismeretekért, segítségért. Továbbá köszönöm osztályfőnökömnek és magyartanáromnak, Horváthné Gyovai Melindának a cikk szerkesztésével kapcsolatos támogatást. Az Egyetem Atomfizika Tanszékén is kaptam segítséget – hálás vagyok Kocsányi László laborvezető közbenjárásáért, valamint Kiss Gábor és Sebők Béla információiért a kondenzátorokkal kapcsolatban. És végül, de nem utolsó sorban köszönöm családomnak a támogatást, bíztatást.