Fizikai Szemle honlap |
Tartalomjegyzék |
Pál Mihály
Bocskai István Gimnázium, Szerencs
Néhány évvel ezelőtt Szakmány Tibor és Papp Katalin cikke keltette fel figyelmemet, amelyben a digitális fényképezőgép tanórai alkalmazását mutatták be. Kipróbáltam és továbbgondoltam a lehetőségeket annak érdekében, hogy demonstrációs órai mérést végezhessünk, de mindenképp egy tanóra alatt. Ennek eredményeit szeretném itt megosztani.
Sok próbálgatás után a következő eszközöket használom demonstrációs mechanikai mérésre: digitális fényképezőgép, számítógép, projektor. Az eszközválasztásban három szempont játszott fő szerepet:
A mérés nem veheti el a tanóra nagy részét, mert ezt a tananyag mennyisége nem engedi meg. A gyakorló tanárok tudják: nem bízhatjuk csak a diákság szorgalmára (és érdeklődésére), hogy a bevezetett fogalmakat, összefüggéseket otthon maguktól megértsék és alkalmazzák, ezért a tanórai idő kincs. Több publikáció is található már az interneten, amelyben digitális fényképezőgép segítségével elemeznek mozgásokat. Úgy látom, ezek közös gyökere a Dede–Isza-féle, a középiskola 2. évfolyamára írt fizikakönyv. Ebben a szerzők a mozgásokat stroboszkópos felvételeken keresztül elemzik. Az akkori fényképezési technológiát jól kihasználták, de a módszer hátránya, hogy nem lehet a kísérlet után rögtön vizsgálni a felvételeket. A már említett dolgozatokban reprodukálni igyekeznek a stroboszkópos felvételeket, mégpedig oly módon, hogy képszerkesztő programok segítségével egy képpé szerkesztik a digitálisan felvett videó képkockáit. Ez a szerzők szerint is több órát vehet igénybe, nem lehet a felvételt ugyanazon az órán kiértékelni. Ezért próbálkoztam az alább bemutatandó módszerrel.
A látványosságon nem a cirkuszias show-t értem, hanem a korosztály számára megszokott és elvárt vizuális technológia alkalmazását. Tapasztalataim szerint nem lehet sikert elérni a taneszközpiacon elterjedt apró, az iskolapadból alig látható műanyag mütyürökkel. Ezek demonstrációra alkalmatlanok. E helyett a felvételek képkockáit projektorral kivetítve, azt mindenki számára jól láthatóvá tehetjük. A diákoknak az is tetszik, hogy magukat látják kísérletezés közben, mintha valamelyik tudományos tv-csatornát néznék.
A tanulók mindennapjaiban szerepel a digitális fényképezőgép, a memóriakártya, a számítógép. Ezek mind olyan tárgyak, amelyek használata tőlük már nem igényel külön figyelmet, sőt jogosan elvárják, hogy mi is ezeket alkalmazzuk. Lehet milliméterpapíron is ábrázolni, és lehet Excel program segítségével is, a diák az utóbbit választja, mert azt jobban ismeri. A cikkben szereplő jelenségeket digitális fényképezőgéppel rögzítjük, a memóriakártyát áttesszük a számítógépbe, médialejátszó programmal lejátszuk, megállítjuk, elindítjuk, léptetjük. Mind olyan tevékenységek, amelyre boldogan jelentkeznek a tanulók, és ezek mellett még a kísérletet is ők végzik. A tanárnak csak előkészítő és irányító szerep jut. A mérések kiértékelését – az órán látottak alapján – otthon önállóan is elvégezhetik, csak a fájlt kell közzé tenni.
Az egyenes vonalú mozgások vizsgálatához egy szalagfüggönysínt, rajta egy csapágygolyót, ütközések elemzéséhez a mechanikai készlet sínjét és kiskocsijait alkalmazom. A síneket helymeghatározás céljából beosztással láttam el, oldalára papír mérőszalagot ragasztottam.
A digitális fényképezőgépek úgy készítenek videót, hogy másodpercenként meghatározott számú képet – úgynevezett frame-et – rögzítenek. Minden fényképezőgép leírásában megtalálható ez a képszám, amely függ a képfelbontástól is. Nekem egy alsókategóriás kompakt gépem van, ezen 640×480 felbontás esetén 30 fps (azaz másodpercenként 30 frame-et készít) beállítás található. Tapasztalataim szerint ez elegendő. Ellenőriztem, hogy a frame-ek tényleg egyenletes időközönként készülnek-e. Ehhez felvételt készítettem egy éppen futó digitális stopperről, és olyan médialejátszóval játszottam le, amely képes frame-enként léptetni. Bármely időpillanatban indítottam el a kockázást, 30 kocka alatt mindig 1 másodperc telt el, 3 kocka alatt pedig 0,1 másodperc. Ez azt jelenti, hogy a digitális fényképezőgép valóban 30 fps sebességgel és egyenletes időközönként készíti a frame-eket. (Ha mégsem teljesen egyenletesek az időközök, az sem fog problémát okozni.) A videó-fájl lejátszásának lényege a kockázás. Rengeteg ilyen lejátszó program létezik, én a VLC médialejátszó ingyenes verzióját használom. Tudom, hogy 1 kocka 1/30 másodperc, így külön időmérésre nincs szükség.
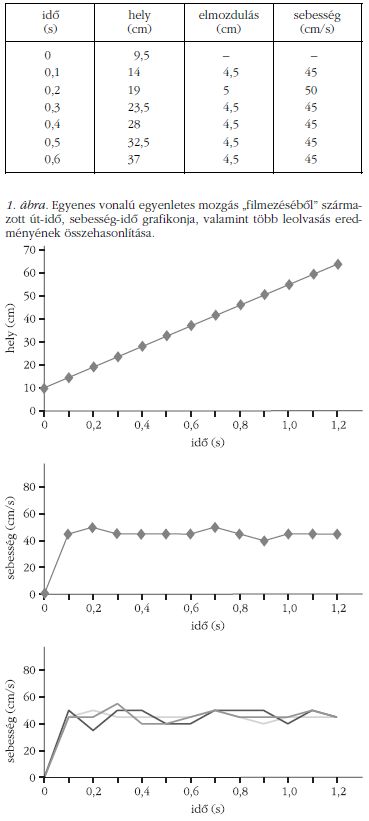
A csapágygolyót végiggurítjuk a vízszintesen elhelyezett sínen, a mozgást felvesszük, majd projektoron keresztül léptetve lejátsszuk (5 perc!). A mozgás sebessége határozza meg, hogy hány képkockánként olvassuk le a golyó helyzetét. Én praktikusan három többszöröseihez ragaszkodom, tudván, hogy 3 képkocka 0,1 másodperc. A golyó helyének leolvasása 1-2 cm-es szórást okoz az osztályban. Ez kedvező alkalom arra, hogy beszéljünk a mérés szubjektív tényezőjéről és a hibáról is. Bátorítom a tanulókat, fogadják el a saját maguk által leolvasott értéket és ne a tanár adatát várják, hiszen előbb megbeszéltük a leolvasás pontatlanságát. Erre ne sajnáljuk az időt, mert itt egy lényeges fogalmat alapozunk meg: a mérést. Táblázatban rögzítjük az idő-hely adatpárokat:
Ezt először mindig kézzel rajzolt táblázatban teszem meg, mert ekkor folyamatában látható a struktúra kialakítása. Kiszámítjuk az egyes időközökhöz tartozó elmozdulásokat, majd ebből a sebességeket is. Rögtön szembetűnik, hogy az elmozdulások és a sebességek közel azonosak. A megtett út pedig egyenletesen növekszik.
Ezt grafikonokkal megerősítjük. Sajnos órán nincs mindenki előtt számítógép, így ők kézzel ábrázolnak, de én táblázatkezelővel is rögzítem az eredményeket.
Az út-idő grafikon elég meggyőző (1. ábra, felül), a sebesség-idő grafikon (1. ábra, középen) bizonytalanságra adhat okot. Erre megkérek két diákot, hogy az én általam leolvasott adatoktól függetlenül írjuk be a táblázatba az ő adataikat is. Ehhez célszerű előre elkészíteni egy üres Excel-táblát, képletekkel, üres grafikonnal, így a hely adatainak megadásával rögtön kirajzolódik az ő mérési eredményük is (1. ábra, alul).
A fent említett 1-2 cm-es leolvasási eltérés más alakú, de ugyanolyan jellegű görbét eredményez. Nem nehéz a tanulókat rávezetni arra, hogy a sebességek átlagával jól jellemezhetjük a mozgást, és a „rendellenességek” a mérés természetes velejárói.
Érdemes több felvételt is készíteni különböző sebességekkel mozgó golyóról. A második mérést már elég csak Excel-táblázattal elemezni. Ennek struktúrája teljesen azonos az első táblázatéval, és a grafikonok pillanatok alatt elkészülnek. A többi két-három felvétel fájlját elérhetővé tehetjük az osztály számára (például Facebook). Ebből mindenkinek fel kell dolgoznia egyet, akár kézzel, akár táblázatkezelővel. Sok digitális feldolgozás szokott születni, amelyet kinyomtatva a füzetbe ragasztanak. Most hivatkozhatnánk az informatikával való interdiszciplináris kapcsolatokra, de a tanulóknak nem azt jelenti, csupán egy mindennapi eszközhasználatot.
A mellékelt táblázatokban és grafikonokban nem szerepel a mennyiségek hagyományos jelölése, csak a mértékegység. Ez direkt készül így. Szeretném elkerülni – legalább az első órákon – hogy pusztán képletalkotás legyen a mérés eredménye. Az egyenletes mozgás képletét úgyis hozzák magukkal az általános iskolából, de úgy tapasztaltam, hogy nem kapcsolódik rögtön össze a kísérleti eredménnyel. Feladatmegoldás során már bennük merül fel a természetes igény a mennyiségek jelölésére, az összefüggések matematikai megfogalmazására. Ekkor „esik le”, hogy ezt már tanulták, csak nem ismerték fel. Ez (ha nem is katartikus) jó érzéssel tölti el a tanulókat: helyükre kerültek a dolgok.
Ezek után jönnek az első meglepetések. A sínt alig észrevehetően lejtős helyzetbe állítom úgy, hogy észre sem veszik és megismételjük a néhány órával ezelőtti mérést. Mi lehet az eltérés oka? Gyorsan felismerik, hogy a sín nem áll vízszintesen, és tapasztalat szerint a lejtőn fel lehet gyorsulni. (Mélyebbre még nem megyünk.)
A táblázat szerint valami baj van: az időegység alatti elmozdulás egyre nő, felül kell vizsgálni eddigi eredményeinket. Most is elkészítjük a táblázatokat, grafikonokat (2. ábra), és a füzetükben meglévő eredményekkel összehasonlítjuk. Szembetűnik a sebesség változása, ezért a táblázatot kiegészítjük ezzel az oszloppal.
Ez az oszlop már nagyobb szórást mutat. Ha Excel-lel dolgozzuk fel az adatokat, akkor könnyen megmutathatjuk, a megtett utat akár csak 1-2 cm-rel megváltoztatjuk a táblázatban, milyen hatalmas eltérések keletkeznek a gyorsulásban.
A gyorsulás grafikon (2. ábra, alul) helyett célszerűbb és didaktikusabb is a sebességgrafikont elemezni. A táblázatkezelő ebben is segítségünkre van, hiszen pillanatok alatt trendvonalat illeszt (2. ábra, középen) az adatokra feltüntetve a gyorsulás értékét is. (Ezt a módszert várják el az emeltszintű érettségi méréseinél is.) Lényegében az átlaggyorsulást olvassuk le a sebesség-idő grafikonról: a = 0,5 m/s2.
A guruló golyó gyorsulását nem ismerjük, de a nehézségi gyorsulásnak jól elfogadott értéke van, ezért a g mérésénél precízebben kell eljárnunk. A mérés elve a gyorsuló mozgáséval azonos, de a gyors mozgás miatt törekedni kell a jó megvilágításra és háttérválasztásra. A digitális fényképezőgépek a "záridőt", vagyis egy – egy képkocka exponálási idejét a fényerősség átlagának megfelelően, automatikusan állítják be, de vannak olyan fényképezőgépek is, amelyeknél manuálisan állíthatjuk a fényérzékenységet. Ezért mindenképpen fehér, erősen megvilágított háttér előtt, sötétszínű golyó esését célszerű felvenni (3. ábra). Erre a legjobb lehetőség egy napsütötte fehér fal, de tanteremben is lehet értékelhető felvételeket készíteni (ekkor számítani kell a golyó elmosódására). Egy nagy csapágygolyó jól megfelel a célnak, ugyanis a közegellenállás hatása a négyzetes törvénnyel számolva meg sem közelíti a helyleolvasás hibáját. Íme, egy tantermi mérés minden hibájával és erényével. (A legnagyobb erénye, hogy meg tudtuk mérni.)
Terjedelmi okokból nem tudok a mérési eljárásból adódó hibáról részletesen szót ejteni, de célszerű a mérés első néhány pontját kihagyni az ábrázolásból (4. ábra), mert a hiba mértéke az idő előrehaladtával csökken.
Nagyon sokféle mérést elvégezhetünk még, ezekből néhányat most csak felsorolni tudok:
A fogalmak méréssel és grafikonnal való bevezetésének hallatlan nagy előnye, hogy a diákoknak nem kell matematikai kifejezésekkel birkózniuk, csak a fizikai lényegre kell figyelniük. Az sem elhanyagolható előnye a grafikonoknak, hogy szemlélteti a mozgás lefolyását, így például könnyebben el tudják képzelni a gyorsuló mozgást a grafikon alapján, mint a négyzetes úttörvény képletén keresztül. Tapasztalataim szerint ezt jól kihasználhatjuk feladatmegoldásban is, "kikerülhetjük" a képletek kizárólagos alkalmazását, amellyel nagy lépést tehetünk a fizika megértése felé.