Fizikai Szemle 2005/10 - Sudár Sándor: SZÁMÍTÓGÉPES SZIMULÁCIÓK ÉS VIZUÁLIS MÓDSZEREK A FIZIKAOKTATÁSBAN

SZÁMÍTÓGÉPES SZIMULÁCIÓK ÉS VIZUÁLIS MÓDSZEREK A FIZIKAOKTATÁSBAN

Sudár Sándor
Debreceni Egyetem, Környezetfizikai Tanszék

A személyi számítógépek megjelenésével a számítógépek a fizikai elôadók kísérleteket bemutató asztalaira kerültek a többi kísérleti eszköz közé, egyrészt a kísérletek támogatására, másrészt olyan fizikai jelenségek szimulációjára, amelyeket egy előadás körülményei között, nem lehet bemutatni. Egyesekben már a kezdeti időkben felmerült az "elvégezhető" kísérleteket is szimulációval helyettesítsék. Szerencsére ezek az elképzelések nem nyertek teret. Sőt például a debreceni fizikatanári képzésben fontos szerephez jutottak a demonstrációs laboratóriumi gyakorlatok, amelyek keretében a hallgatók maguk is elvégezték az előadáson szereplő alapvető kísérleteket. (A jelenlegi felsőoktatási "normatív" finanszírozási rendszer, amely csak a hallgatói létszámokat veszi figyelembe, nyilvánvalóan a gyakorlatok megszüntetése irányába kényszeríti az oktatást, mivel azok mind eszköz-, mind bérköltségben a legdrágábbak. Szomorúan várom azt az időt, amikor a fizikatanár csak számítógépes szimulációval végzett kísérleteket, vagy vegyész csak számítógéppel gyakorolta a víz és kénsav elegyítését. Igaz, így ha felrobbanna az elegy, senki sem sérülne meg.)

Mielőtt valaki az gondolná, hogy a szimulációk ellenzői közé tartozom, szeretném kijelenteni, hogy éppen ellenkezőleg: az okos és hasznos szimulációk alkalmazását igen fontosnak tartom. Életünk nagyon sok területén, különösen, amikor a jövőről próbálunk valamit megállapítani, nincs is más lehetőségünk, mint szimulációra alapozni. Itt mindig a szimuláció mögött álló modell határozza meg, hogy a jóslat és a valóság mennyire fog egybeesni. Negatív példaként említhetném az időjárás-előrejelzést, amikor még hatalmas számítógépes rendszerek és műholdas megfigyelés mellett is korlátozottak az eredmények. Ugyanakkor más területeken, például a hidrológiában vízbázisok jellemzőinek változására, vagy szennyezések terjedésére jobb modellekkel rendelkezünk. Egy konkrét példa: a tervezett ITER fúziós reaktorhoz (néhány hónapja egyeztek csak meg, hogy Franciaországban lesz)¹ készült egy karbantartó robot szimulációja, amely a plazmatároló gyűrű belsejébe kis nyíláson belépve, felépíti saját eszközeit, valamint pályáját a gyűrűben, és kicseréli a szükséges belső falelemeket.

1. ábra. Az MIT TEAL (Technology for Active Learning) stúdiója

A fizikaoktatásban a vizuális technikák (szimulációk és animációk) és számítógéppel támogatott méréstechnika alkalmazásának megfelelő egyensúlya adhat megoldást az ismeretek hatékonyabb átadására. Az oktatás hatékonysága természetesen nem csak nálunk probléma. A Massachusetts Institute of Technology (MIT) Fizikai Intézeténél is ugyanazokkal a problémákkal találkoztak a nem fizika szakos hallgatók oktatásában, mint mi: az előadást látogató hallgatói létszám a szemeszter során kevesebb mint a felére csökken, a szemesztert eredménytelenül zárók aránya magas. A hallgatók unalmasnak, száraznak tekintik a fizikát. Ôk a megoldást olyan integrált oktatási formában látják, amely egyesíti az előadást és a gyakorlatot. A tananyag felhasználja a különböző szimulációs és animációs módszereket, az előadás/gyakorlat részeként a hallgatók egyidejűleg végzik a számítógéppel támogatott kísérleteket. A stúdiónak nevezett oktatóterem az 1. ábrán látható. A teremben 8 számítógépes kivetítő található, a normál táblákat kamerák nézik, amelyek képe a kivetítőre kerül. 3-3 hallgató dolgozik egy kísérleti eszközcsomaggal. Az előadás és a gyakorlat egységet képez. A hallgatóknak az előadás előtti napon, a hálózaton keresztül, kérdéseket kell megválaszolniuk az előző előadás anyagából, valamint az adott előadáshoz kapcsolódó fogalmakból. A válaszokat számítógép értékeli. A foglakozás keretében is kapnak további kérdéseket, amelyek végül szintén beszámítanak a félév végi érdemjegybe. A kísérlet már néhány éve folyik, és felmérések szerint a hallgatók igen jó véleménnyel vannak a projektről. Különösen a két- és háromdimenziós szimulációs modelleket kedvelik, amelyek könyvekben nyilvánvalóan nem jeleníthetők meg. A projekt részletei a következő honlapon találhatók:
http://ocw.mit.edu/OcwWeb/Physics/8-02TSpring-2005/CourseHome/index.htm. Jelenlegi körülmények között a koncepció egésze nálunk nem valósítható meg, de bizonyos elemei, például a webes kikérdezés, vagy a két- és háromdimenziós szimulációs modellek alkalmazása megoldható. Ez azért is megvalósítható, mert a világ fizikusai, fizikatanárai már jelentős munkát fektettek e témába. A cikk célja a fizikai szimulációk, animációk témakörébe tartozó internetes források egy részének a megismertetése.

Ha a Google internetes keresőprogramot megkérdezzük azon honlapokról, amelyek a fizika és a szimuláció szavakat tartalmazzák (physics +simulation) a válasz szerint 8 270 000 ilyen honlap található a kereső által ismert weblapok között. Tovább szűkítve az oktatás (+teaching) szóval, még mindig reménytelenül sok, 632 000 honlap található. Ezek mindegyikének megtekintése is túl nagy feladat volna, így inkább az általam megtalált néhány hasznos forrást ismertetem, ahonnan elindulva további érdekes és felhasználható szimulációkhoz juthatunk. Hozzáférhetőség szempontjából a szimulációkat három csoportba sorolnám: a) fizetni kell érte, b) az interneten keresztül szabadon használható, de nem lehet letölteni a saját számítógépünkre, és ennél fogva nem is módosítható (pl. kínai feliratokkal van ellátva), c) szabadon letölthető és módosítható (a forrás megjelölésével). Az a) csoporttal nem akarok foglalkozni, csak megjegyzem, a pénzkérés nem garancia a minőségre. A b) korlátozott használhatóságot jelent a magyar tannyelvű oktatásban, állandó internetkapcsolat kell hozzá, és nehezebb beépíteni egy előadásba. Így elsősorban néhány, a c) csoportba tartozó forrást szeretnék bemutatni.

2. ábra. A munkaterületen tetszőleges számú pozitív és/vagy negatív töltés helyezhető el, amelyek bárhova elmozgathatók. A sztatikus teret térerősség-vonalakkal, illetve térvektorokkal lehet jellemezni. Ez utóbbiak a kis vektorjelek az ábrán, amelyek az adott pontban megadják a térerősség irányát. A térerősség nagyságát a vektor színe jelzi. Elhelyezhető még egy mozgatható próbatöltés is, amellyel tetszőleges pontban megkaphatjuk az elektromos térerősség nagyságát és irányát (fekete pont). A lejátszás (Play) elindításával láthatóvá tehető a próbatöltés
3. ábra. Töltött test elektromos tere egy vezetőből készült doboz belsejében. A töltött test nagysága, alakja, helyzete változtatható. Az applet a Poisson-egyenletet oldja meg, az adott határfeltételekkel. A jobb oldali részben látható a síkbeli probléma geometriája, az elektromos térerősséget térvektorok mutatják. A folytonos görbék az ekvipotenciális felületek. Baloldalt a potenciálfüggvény látható térben (ez tetszőlegesen forgatható a térben). A bal oldali ábrán a potenciál helyett a töltéseloszlás is megjeleníthető (a töltéseloszlás a vezető felületén). A vegyes magyar- angol feliratok abból származnak, hogy a honlap szövege módosítható, míg az applethez tartozó feliratok nem.

Mielőtt a világban található ilyen forrásokra térnék, meg kell említeni egy biztosan sokak által ismert magyar honlapot (http://titan.physx.u-szeged.hu/~serenyi/ph14hu/), amely egy német honlap, a http://www.walter-fendt.de/ fizika részének magyar változata. Az itt található 46 alkalmazás lefedi a fizika teljes területét, azaz minden témakörre csak néhány alkalmazás jut. (Az itt ismertetett fizikai szimulációk 17 nyelvi változatban találhatók meg, ami használatuk elterjedtségét mutatja.) Az alkalmazások interaktív módon befolyásolhatók, a működés paraméterei beállíthatók.

Mi van ezen alkalmazások mögött? A SUN Microsystem Java programozási nyelve, amely hordozható a különböző számítógépek és operációs rendszerek világában. Futtatásukhoz azonban az adott operációs rendszerhez tartozó futtatási környezet szükséges. A Java-programoknak két változata van: az egyik a normál Java-program, amely ugyanúgy működik, mint bármely más nyelven megírt program (kivéve a hordozhatóságot), míg a másik az úgynevezett "Java-applet", amelyet az interneten való felhasználásra terveztek. Amikor rákattintunk egy ilyen alkalmazásra, az letöltődik a számítógépünkre, és a mi gépünkön fut. Azonban nem tud a gépünkön adatot megváltoztatni, sem onnan kiolvasni vagy továbbítani. A fenti alkalmazások is ilyen Java-appletek, biztonságosan futtathatók. Ráadásul a fenti honlapról ezek le is tölthetők, és így internetkapcsolat nélkül is használhatók. (Windows XP SP2 alatt azonban állandó figyelmeztetést kapunk az aktív tartalom futtatása miatt.) Az elérhető szimulációk legnagyobb része ilyen Java-appletből áll, de természetesen találhatunk rendes, végrehajtható programokat is. Mielőtt bárki megijedne, hogy most akkor meg kell tanulnunk Java nyelven programozni, szeretnék mindenkit megnyugtatni, hogy ez nem feltétlenül szükséges. A hozzáférhető appletek felhasználásával sok mindent elkészíthetünk. Sőt, alkalmas programozási környezetben anélkül tudunk Java nyelven programot készíteni, hogy ismernénk a programozási nyelvet. (Természetesen ez nem jelenti azt, semmit sem kell tanulni.)

4. ábra. Az EJS bejelentkező ablaka
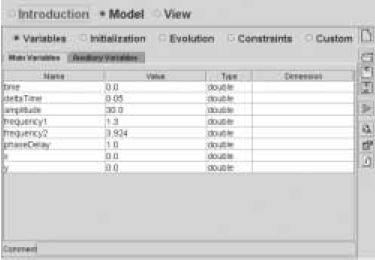5. ábra. Az EJS "Model" ablaka, mely a probléma matematikai leírását tartalmazza.

Az appletek kezelése legegyszerűbb egy weblapon keresztül. A weblap segítségével be lehet állítani az appletek paramétereit. Az egyik legismertebb, legelterjedtebb fizikai szimulációs appletcsomag W. Christian (Davidson College) Physlets összeállítása: http://webphysics.davidson.edu/applets/applets.html. Az appletek letölthetők és oktatási célra szabadon felhasználhatók. A szerzők oktatási anyagokat is készítettek, amelyek könyv alakban megvásárolhatók, és a könyvhöz mellékelt CD-n kidolgozott megoldások találhatók. Azonban az interneten nagyon sok, a fenti appletekkel készült szimuláció található. A 2. és 3. ábrán két ilyen, a sztatikus elektromos tér bemutatására használható és a fenti appleteket alkalmazó megoldás látható. Ez két példa a Physlets-appleteket használja. A név könnyen kitalálhatóan a Physics applets rövidítéséből származik. Ezek nagyon sok, különböző nyelvű honlapon megtalálhatók. A Physletsek német honlapján (http://pen.physik.uni-kl.de/physlets/index.html.de) kereső is található, amely körülbelül 5000 weblapot ismer a világon, valamint 3000, egyéb fizikai szimulációval foglalkozó Java-appletet. Ezek a kereső segítségével le is tölthetők. Ugyanitt találhatók és letölthetők az úgynevezett "Physlet scriptor"-ok, amelyek segítségével néhány egérkattintással előállítható egy weblap megfelelően konfigurált, több appletet is használó szimulációval, a bemeneti adatok beállításával.

Egy másik nagy projekt az Open Source Physics (http://www.opensourcephysics.org/), amely szabadon felhasználható tananyagok, tanmenetek készítését is célul tűzte ki. Részben a Physletsek felhasználásával, mint például a http://stp.clarku.edu/simulations/ weblap, amely statisztikus fizikai és hőtani szimulációkat tartalmaz. Ezek mellett két független fejlesztésű programcsomag is megtalálható itt.

Az egyik az Easy Java Simulation (http://fem.um.es/Ejs/) a Java nyelvre alapozott saját szimuláció elkészítésére ad lehetőséget azoknak, akik meg tudják fogalmazni matematikailag a szimulációs problémát. Az EJS ebből készít egy Java-programot, egy Java-appletet és egy alap weblapot. Maga az EJS program is Java nyelven készült, így bármely Java fejlesztőrendszerrel rendelkező operációs rendszer alatt futtatható (Windows, Linux, bármely UNIX verzió stb.). A 4. ábrán az EJS bejelentkező ablaka látható, ennek tartalma lesz a weblap szöveges része. Az ábrán a programcsomaghoz mellékelt, a Lissajous-görbéket előállító mintapélda bevezető oldala látható. A tényleges modell elkészítéséhez a másik két lapot kell kitölteni. A "Model" ablakban kell megfogalmazni a problémát (5. ábra). Itt kell definiálni a változókat, a matematikai egyenleteket, amelyek ezeket összekapcsolják: időben hogyan változnak a mennyiségek (Evolution ), milyen egyéb feltételeknek kell eleget tenni. Az időbeli változásnál differenciálegyenlettel leírt kapcsolat is megadható, akkor automatikusan generálja hozzá a numerikus differenciálegyenlet megoldási algoritmusát.

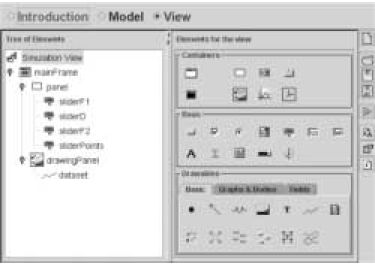6. ábra. Az EJS "View" menüje. Itt kell az objektumokat a megjelenítendő ablakban elhelyezni és összekapcsolni a változókkal.
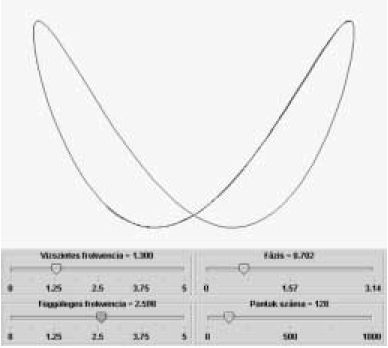7. ábra. A Lissajuos-görbéket megjelenítő program eredményablaka

A harmadik - és talán a legfontosabb - rész a numerikus változók összekapcsolása a megjelenítendő objektumokkal (View ), amely a 6. ábrán látható. A 7. ábrán az előző ábrákon bemutatott-megfogalmazott szimuláció eredménye látható egy adott pillanatban. A feliratok - némi kompromisszummal - magyar nyelvűek is lehetnek. A programhoz angol nyelvű leírás tartozik, amely példákon keresztül mutatja be annak használatát. Aki rendelkezik programozási ismeretekkel, néhány óra alatt elsajátíthatja az alapokat.

8. ábra. Két korong ütközése légpárnás asztalon. (Sajnos a színes ábra szürkébe transzformált képén nem minden látszik.)
9. ábra. Az egyik korong helykoordinátái az idő függvényében, az ütközésről készült felvétel alapján.

Az Open Source Physics másik fontos programcsomagja, amely kevésbé tartozik a jelen témakörbe, a mérési adatok, főleg videofelvételek digitális feldolgozására alkalmas Tacker program. Alapvetően a légpárnás mechanikai kísérletek feldolgozását segíti. A 8. ábrán két korong ütközéséről készült felvétel egy pillanata látható, bejelölve rajta az egyes korongok, valamint a két testből álló rendszer tömegközéppontjának nyomvonala. A nyomvonal meghatározásához a program lehetővé teszi videofelvétel feldolgozását különböző "szűrők" alkalmazásával. A 9. ábrán az előző felvétel feldolgozásának korábbi lépése látható. Egy szűrő segítségével az eredeti videofelvételből előállítható a 9. ábra bal oldalán látható kép, amikor a mozgás egyes fázisainak képe egymásra van másolva. Ezen kép segítségével meghatározhatók a nyomvonal egyes pontjai. Ezeket a felhasználónak manuálisan kell a képhez rendelnie. A pontok bejelölése után automatikusan meghatározza a nyomvonalon lévő pontok helyzetét, ezekből különböző grafikonok és táblázatok is előállíthatók. Az időskálát a másodpercenkénti felvételek száma határozza meg. A 9. ábrán az egyik test helyzetének koordinátái láthatók az idő függvényében. Ezen elsődleges adatok és az ezekből számítható mechanikai mennyiségek (sebesség, lendület, gyorsulás, erő komponensei, derékszögű és poláris koordináta-rendszerben) ábrázolhatók tetszőleges párosításban. A nyomképen megjeleníthetők az egyes vektormennyiségek is (sebesség, lendület, erő). Mind az idő, mind a térbeli skála kalibrálható. Az alkalmazott koordináta-rendszer tetszőlegesen pozicionálható, elforgatható. A mechanika légpárnás asztalon elvégezhető kísérleteinek kiértékelésére igen alkalmasnak látszik. Meglepő módon a program egy másik feladat megoldására is alkalmas: optikai spektrumok intenzitásviszonyainak kiértékelésére is felkészítették.

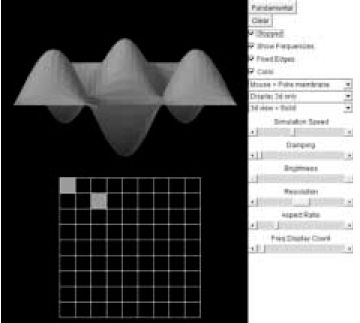10. ábra. Membrán rezgése, különböző rezgésmódjai (Paul Falstad)
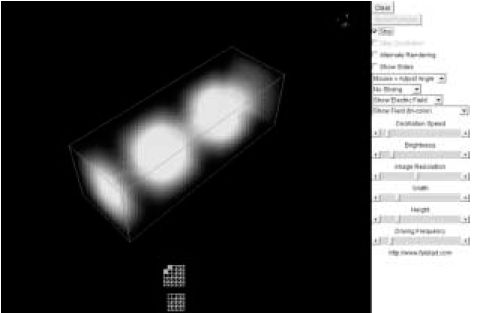11. ábra. Elektromágneses hullámok terjedése hullámvezetőben

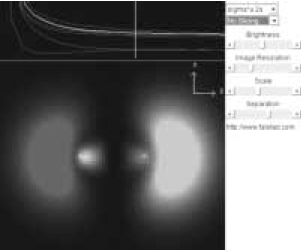12. ábra. Hidrogénmolekula hullámfüggvényei
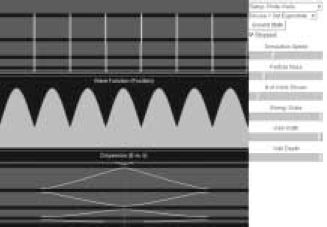13. ábra. Kristályrács egydimenziós kvantummechanikai modellje

Az előzőekben bemutatott szimulációk mellett az egyik, sokak által nagyra értékelt honlap, Paul Falstad fizikai és matematikai appleteket tartalmazó programjaira (http://www.falstad.com/mathphysics.html ) szeretném felhívni a figyelmet. Az appletek letölthetők, és a hozzájuk mellékelt weblappal futtathatók. Néhány témakör a weblapon található szimulációkból: rezgések és hullámok, akusztika (10. ábra), jelfeldolgozás (Fourier-sor, digitális szűrés), sztatikus elektromágneses tér, elektrodinamika (hullámvezetők (11. ábra), üregrezonátorok stb.), kvantummechanika (hidrogénatom, molekulapályák (12. ábra), dipól átmenet, háromdimenziós rezgés, kristályrács (13. ábra) stb.), lineáris algebra, vektorszámítás stb. Általában egy applet több különböző, de azonosan kezelhető probléma szimulációját tartalmazza. A 10-14. ábrán látható néhány példa természetesen csak egy pillanatfelvétel a színes, mozgó és a problémához tartozó, változtatható paraméterekkel futtatható szimulációkról.

14. ábra. Ponttöltés állandó erősségű elektromos terének eredője az MIT által kidolgozott téranimációval.
15. ábra. A Faraday- és Lenz-törvény Java-applettel megvalósított szimulációja. Egy álló állandó mágneshez egy szabadon eső, rövidre zárt tekercs (gyűrű) közeledik. Természetesen ez csak egy pillanatfelvétel. A tekercs ellenállása változtatható, az ábra egy szupravezető gyűrű esetét mutatja. Ebben az esetben a tekercs visszapattan a mágnesről. A tekercsben folyó áram a jobb alsó sarokban lévő grafikonon látható.

A bevezető részben említett MIT-projekt tananyaga az OpenCourseWare keretében elérhető a interneten (http://ocw.mit.edu/index.html), ezekbe beágyazva megtalálhatók a különböző animációk és szimulációk. Ezekből a 14. és a 15. ábrán mutatok egy-egy példát.

Két további ábra (16., 17. ), a Californian Institute of Technology (CalTech) (http://www.pma.caltech.edu/physicscourses.html) fizikaoktatásában alkalmazott Java-appletekből mutat két példát (http://www.cco.caltech.edu/%7Ephys1/java.html).

16. ábra. Sztatikus elektromos tér szimulációja Java-aplettel (CalTech).
17. ábra. Körmozgást végző töltés elektromos tere adott pillanatban.
Az applet lehetővé teszi az elektromos tér vizsgálatát különböző feltételek esetén.

A CalTech appletjei sajnos nem tölthetők le, csak az interneten keresztül használhatók.

További néhány, megtekintésre érdemes weblap:

http://pen.physik.uni-kl.de/
http://pen.physik.uni-kl.de/medien/MM_Videos/index.html
http://www.colos.org/
http://webphysics.davidson.edu/physletprob/ch7_in_class/in_class7_2/default.html
http://www.schulphysik.de/
http://www.jhu.edu/~signals/index.html
http://suhep.phy.syr.edu/courses/vrml/electromagnetism/index3.html

A fentiekből is látható, hogy fizikusok, fizikatanárok közösségei a világ minden táján dolgoznak a fizikaoktatás korszerűsítésén, felhasználva azokat a technikai, informatikai eszközöket, amelyek hozzáférhetővé váltak az elmúlt években. A fizika a természet vizsgálatával foglalkozik, ezért a kísérleteket nem helyettesíthetik a szimulációk, ugyanakkor a szimulációk elősegíthetik a kísérletek és a fizikai modellek jobb megértését.

___________________________________

1 Lásd ZOLETNIK SÁNDOR: Szabályozott magfúziómágneses összetartással I-II. - Fiz. Szle. 55/3 (2005) 100, 55/7 (2005) 234 és JÉKI LÁSZLÓ: Megállapodás az ITER felépítéséről - Fiz. Szle. 55/8 (2005) 296

Fizikai Szemle honlap

Tartalomjegyzék

SZÁMÍTÓGÉPES SZIMULÁCIÓK ÉS VIZUÁLIS MÓDSZEREK A FIZIKAOKTATÁSBAN