Fizikai Szemle honlap |
Tartalomjegyzék |
Radnóti Katalin
ELTE TTK Fizikai Intézet
Írásunk első, bevezető részében általánosságban foglalkozunk az analógiával és a gondolkodásban, a megismerésben betöltött szerepével. Ezt követően bemutatunk néhány példát a fizika történetéből, majd az analógia fizika oktatásában betöltött szerepére koncentrálunk sok érdekes példa felhasználásával.
Az eredeti görög αναλoγoσ kifejezés számok közötti viszonyt, összemérhetőséget, arányt jelentett. Eukleidész V. könyve a viszonyok hasonlóságaként értelmezi: "az arányosság" (αναλoγια), "az arányok hasonlósága" olvasható a definíciók közt.
Az emberi gondolkodás alapvetően analógiás típusú, minden, számára új jelenséget már ismert kognitív struktúrákkal való analógia alapján ragad meg. Ez az a gondolkodásforma, amely a legjobban áthatja a megismerés más területeit, segíti a megértést, a fogalomelsajátítást és a problémamegoldást.
Két rendszer analóg, ha megfelelő részeik világosan megfogalmazható kapcsolataikban megegyeznek. Az analógiák előfordulnak a mindennapi gondolkodásban, a gondolkodás és a magyarázat eszközei, segítik a problémamegoldást, az új helyzet megértését a tanulásban és a tudományos felfedezésekben.
Az analógiával való gondolkodás a meglévő tudás felelevenítéséből áll, azért, hogy megértsük a számunkra ismeretlen, új információkat. Az analógia az emberi gondolkodás alapját képező mechanizmusok egyike. Minden értelmi cselekvés analógiás gondolkodást foglal magában, az analógia a kognitív képességek alapja, és az analógiás gondolkodás az intelligencia egyik fontos jellemzője. Az analógiák segítik az információk összekapcsolását és ezzel az átfogó, integrált tudásstruktúrák kiépítését [1].
A tudományban analógiát használunk akkor, amikor új hipotéziseket alkotunk, és amikor új tudományos közléseket vitatunk meg. Az analógiáknak nagy szerepe volt több fizikai jellegű felismerés létrejöttében. Írásunk következő részében a fizika történetéből keresünk példákat az analógiák alkalmazására. A klasszikus fizika megalkotói számos példát mutattak erre.
Az utóbbi évszázad során a természettudomány minden területén alapelvvé vált az analógiák, a különféle jelenségek közös törvényeinek kutatása. Egységes elmélettel magyarázhatók a különféle rezgések, legyen az elektromágneses hullám vagy a hang terjedése, de akár valamely gép rezgése. A statisztikus fizika módszerei alkalmazhatók különféle (nagy elemszámú, nem feltétlenül fizikai) rendszerek leírására is. Néhány éve a fizikai analógiák a biológiai evolúció modellezésében is segítenek.
A tudomány nemcsak felhasználja az analógiákat, hanem foglalkozik a jelenségek hasonlósági feltételének megfogalmazásával is.
A modellek is az analógia egyik fajtájának tekinthetők. A tudományos modell utánozza, szimulálja a vizsgált rendszer viselkedését. A modell és a modellezett rendszer működésbeli azonossága egyszerűsítéseken, hasonlóságokon alapszik, és a modellezett bonyolult rendszer magyarázatára, valamint működésének kiszámítására, megjóslására használjuk. A tudományos elméletek lényegüket illetően mindig ilyen modellek.
A természeti törvények, igazságok az ember alkotásai, nem a külső valóság létezői, amelyek felfedezésre várnak, hanem modellek, olyan emberi konstrukciók, amelyek működtetve képesek a természet egy korlátozott területén néhány jelenség lezajlásának korlátozott magyarázatára, jövőbeli történések bizonyos valószínűségű predikciójára, megjóslására. A modelleknek elsősorban gyakorlati hasznuk van, ez lehet egy jó hajózási térkép, vagy csupán értelmes magyarázat arról, hogy a Nap valószínűleg holnap is felkel [2].
A modell olyan gondolati struktúra, amellyel a természeti jelenségek egy jól körülhatárolt csoportját a tapasztalat segítségével úgy írjuk le - sokszor matematikailag -, hogy minden a vizsgált probléma szempontjából lényegtelen hatást elhanyagolunk. Például a Galilei által vizsgált szabadesésnél eltekintünk a légellenállás hatásától. A matematika nyelvén mindig csak a modellel adott természeti jelenség tárgyalható. Ebben az esetben ez a szabadesés, amely a négyzetes úttörvény egyik ismert esete, amikor s = g t2/2. A természet bonyolultsága így egyetlen lépésben nem ragadható meg. A modellek finomításával, amely a legtöbb esetben a matematika egyre erősebb bevonását is jelenti, a természetleírás egyre pontosabb lesz. A kvantitatív magyarázat azonban egyúttal jóslási lehetőséget is ad. Ez azt jelenti, hogy a jelenséget nemcsak hogy megmagyarázzuk, hanem adott fizikai helyzetben az eredményt előre ki is tudjuk számítani. Jelen példánkban egy adott időtartam alatt megtett utat.
Érdekes az 1/r2-es távolságfüggés megjelenése több esetben, amikor a testek pontszerűnek tekinthetők, mint például a Newton-féle gravitációs törvény, a Coulomb-törvény, a gyertyafény intenzitásának változása stb. Az egyszerű geometriai magyarázatához, szemléltetéshez vezessünk be bármilyen erővonalrendszert, amelyeket a pontszerű forrásból indítjuk adott számban, majd különböző r távolságokban vizsgáljuk azt, hogy egységnyi felületen hány megy keresztül, amelyet a tér erősségének feleltetünk meg. Világos, hogyha például különböző sugarú, koncentrikus gömbökkel vesszük körül a pontszerűnek tekintett töltést (tömeget), amely a gömbök középpontjában van, akkor a távolság növekedésével csökken az egységnyi felületen átmenő erővonalak száma. Mivel a gömb felszíne 4πr2 alapján számolható, vagyis négyzetesen nő, tehát az egységnyi felületen átmenő erővonalak számának ilyen arányban kell csökkennie. A történet szerint Coulomb valójában nem is mérte ki pontosan erőtörvényét, egyszerűen a fenti gondolatmenetre alapozva írta fel.
Analógiás kérdésfeltevés vezette Becquerelt is a radioaktivitás jelenségének felfedezéséhez, amely a következő volt: vajon nem lehetséges-e, hogy napfény hatására minden fluoreszcens anyagból röntgensugárzáshoz hasonló sugárzás indul ki?
Ezért kezdte el Becquerel vizsgálni az uránsókat, és kitenni azokat a napra. Az már más kérdés, hogy ez nem igazolódott be, hanem egy teljesen új tudományterület kialakulásához vezetett.
Nézzünk kissé bonyolultabb esetet, amikor a mezőt kialakító mennyiségeket egy egyenes mentén rendezzük el, miként alakul az általuk kialakított mező, amelyet úgy kaphatunk meg, hogy a sok-sok pontszerű töltés, illetve "áramelem-vektor" által kialakított térerősséget összegezzük.
Töltött egyenes vezető által kialakított elektromos mező: vegyük körül a σ töltéssűrűségű vezetődarabot l hosszúságban és r távolságban egy hengerrel!
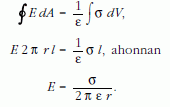
Áramjárta egyenes vezető mágneses tere: a vezetőben folyó áram erőssége I, és az r távolságban a mágneses indukció értéke a gerjesztési törvény alkalmazásával:
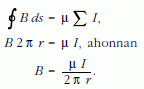
Mindkét esetben 1/r -es távolságfüggés adódik. Az egyik esetben a sok, pontszerűnek vélt elemi töltés által kialakított elektromos mező, míg a másik esetben a sok, szintén pontszerűnek tekinthető áramelem- vektor által kialakított mágneses mező esetében azonos a távolságfüggés. A mező szerkezete természetesen más. Az elektromos erővonalak az elektromosan töltött vezetőre merőlegesek, irányításuk a töltés előjelétől függ. Ezzel szemben a mágneses indukcióvonalak körkörös szerkezetűnek képzelhetők.
Az elektromos és a hőtani jelenségek megértése közel azonos időszakban kezdődött el. Mindkét esetben valamilyen áramló fluidumot képzeltek hozzá. Ezen elképzelés maradványa az, hogy mind a töltés, mind pedig a hő jelölésére a Q betűt használjuk napjainkban is.
Valójában ennél mélyebbre is tekinthetünk. A newtoni fizika jellegzetes gondolkodásmódja alapján a hasonló jelenségek leírásához sok esetben használunk hasonló differenciálegyenleteket. Nézzünk erre példát!
Tételezzük fel, hogy egy testre az állandó nagyságú és irányú F erő mellett súrlódási erő is hat, amely legyen arányos a test sebességével. Itt konkrétan lehet gondolni egy, a levegőben vagy folyadékban eső tárgyra, vagy a fémekben feszültség hatására mozgó elektronokra, amelyet a közismert Ohm-törvény fejez ki. A mozgásegyenlet a következőképp írható fel:
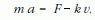
Osszuk el az egyenlet mindkét oldalát az m tömeggel és írjuk fel a gyorsulást a sebesség idő szerinti deriváltjaként, mivel a mozgásegyenletben a sebesség szerepel és a v (t) függvényre vagyunk kíváncsiak:
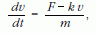
válasszuk szét a változókat és végezzük el az integrálást:
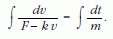
Az integrációs állandó meghatározásához használjuk fel a kezdeti feltételeket, nevezetesen azt, hogy t = 0 időpillanatban a test nulla kezdősebességgel indul. Megoldásfüggvényünk a következőképp néz ki:
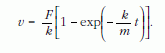
Azt láthatjuk tehát, hogy a sebesség egy darabig nő az idő függvényében, majd aszimpotikusan tart egy állandó értékhez, ami a v » F/k.
Az elektromos és a mechanikai jelenségek hasonló tulajdonságokat mutatnak. Nemcsak a tömegek és rugók alkotnak lineáris rendszereket, amelyeket lineáris differenciálegyenletekkel lehet leírni, hanem a lineáris áramköröknek nevezett elektromos rendszerek is, amelyek teljesen analógok a mechanikai rendszerekkel.
A mechanikai rendszereknek egy másik jellegzetes tulajdonsága a tehetetlenség, amelynek szintén megvan az elektromos megfelelője. Ez akkor jelentkezik feltűnően, amikor egy áramkörben indukciós tekercs van. Ha az indukciós tekercsben egyszer már folyik az elektromos áram, akkor az a feszültség kikapcsolásakor sem akar "megállni", bekapcsoláskor pedig nehezen indul meg az áram.
Teljesen azonos a leírásmódja egy tekercs áramkörbe való bekapcsolásának. Ekkor az áramerősség növekedésékor az áramforrás U feszültségével - Lenz törvénye értelmében - ellentétes irányú Ui önindukciós feszültség keletkezik, amely megakadályozza az áram gyors növekedését.
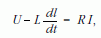
amely elsőrendű differenciálegyenlet a meghatározandó I (t) áramerősség számára. Vegyük észre, hogy egyenletünk teljesen úgy néz ki, mint amilyent a sebességgel arányos súrlódási erő esetében oldottunk meg. Kezdeti feltételeink legyenek a t = 0 időpillanatban I (0) = 0. A megoldásfüggvény ekkor a mechanikai probléma megoldásának mintájára:
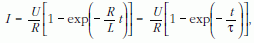
ahol τ = L /R az áramkör időállandója.
A sorba kapcsolt ohmos ellenállás, önindukciós tekercs és kondenzátor esetét nevezzük soros RLC-körnek. Kérdésünk az lesz, hogy ha a végpontokra U = U0 sinωt váltakozó feszültséget kapcsolunk, a körben mekkora áram folyik. Írjuk fel az áramkör egyes elemeire eső feszültségeket:
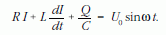
Differenciáljuk az egész egyenletet az idő szerint és használjuk fel, hogy I = dQ/dt
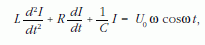
amely másodrendű differenciálegyenlet a keresett I áramerősség számára. A soros RLC-kör differenciálegyenlete teljesen analóg a kényszerrezgések esetében felírható differenciálegyenlettel. Az elektromos és a mechanikai rezgések analóg fogalmait az 1. táblázatban mutatjuk be.
Bármit is vezetünk le egyik vagy másik rendszerre vonatkozóan, az a megfelelő analogont tekintetbe véve mindkét rendszerre igaz lesz. Például egy bonyolult, nagyszámú kapcsolási elemet tartalmazó mechanikai rendszert utánozva nagyszámú ellenállást, tekercset és kondenzátort kapcsolunk össze. De mi az előnye ennek a módszernek? A matematikai feladat ugyanaz, azonban az elektromos áramkört könnyebb elkészíteni és ezen elektromos rendszer paramétereit változtatni. A módszert használják például gépkocsik tervezésénél. Tudni szeretnék, hogy a megtervezett autó valamely adott úton mennyire fog rázkódni. Elektromos áramkört építenek, amelybe indukciós tekercset tesznek, tekintetbe véve a kerekek tehetetlenségét és kondenzátorokat a kerékrugók rugóállandóinak, ellenállásokat a lökésgátlók reprezentálására stb. A rázós utat egy generátorból származó jelsorozattal lehet helyettesíteni. Ez feszültséget kapcsol az áramkörre és megmérve a töltést a megfelelő kondenzátoron, megállapítható az, hogy például a bal első kerék mennyire ugrál. A megfelelő módosítást könnyen el lehet végezni, mondjuk egy kar elforgatásával, amellyel a kondenzátor kapacitása változtatható. Vagyis nem kell ténylegesen megépíteni az autót és abban cserélgetni az alkatrészeket! Természetesen az autó összes jellemzője nem határozható meg ezzel a módszerrel, de akkor is jelentősen leegyszerűsíti az adott probléma vizsgálatát.
Az analógiás gondolkodási forma nagyon jellemző az emberekre. Ez a fajta gondolkodásmód hatékonyan segíti a bárhonnan származó előzetes ismeretek és az új ismeret közti kapcsolatok kiépítését, amely fontos folyamat a jól szervezett, sokféle szituációban előhívható, alkalmazható tudásrendszer kiépítéséhez. Ezért írásunk következő részében ezt vizsgáljuk különböző tankönyvek esetében.
Nevelési szempontból a mindennapi élet problémáinak kontextusába helyezett analógiák a legjelentősebbek. Az iskolai tanítás egyik fontos célja az ismeret, a tudás egyik területről a másikra való transzferálása képességének fejlesztése, a közöttük lévő hasonlóságok kiemelésével azért, hogy a tanulók sikeresen meg tudjanak birkózni az új szituációkkal. Ezért a kreatív gondolkodás fejlesztésének különböző formái is az analógiák alkalmazásán alapulnak.
Az analógiák mint oktatási eszközök segítik a tanulókat az új információ megszerzésében azáltal, hogy felhasználják, amit már tudnak. Az analógiák alkalmazása a tanulók körében az új tartalmak megtanulásának segítése céljából akkor hatékony, amikor egy utalás segíti, hogy a diákok leképezzék az ismerős szituációt az új szituációra. Tehát fontos, hogy a tanárok kellő figyelmet fordítsanak a már elsajátított ismeretek és az új szituáció közötti kapcsolatok tisztázására. Továbbá be kell mutatni az analógiák alkalmazásának határait, hiszen hasonlóságról, nem pedig teljes azonosságról van szó! [1]
Az oktatás során sokszor jelent nehézséget a fizikában használt modellek és a valóság kapcsolata; mikor mit hanyagolunk el, milyen közelítő leírást alkalmazhatunk egy adott probléma vizsgálata esetében. A fizika jellegzetes modelljei például az anyagi pont, merev test, nyújthatatlan fonál, súrlódásmentes lejtő, ideális gáz, és sorolhatnánk a példákat. Valószínűleg célszerű lenne tudatosítani a diákokban a fizikának ezt a jellegzetességét!
Az alábbi két példa rendkívül fontos az analógia és a vizsgált dolgok különbözőségének szemléltetésére [3]:
A tanítás során bátrabban kellene új, szemléletes analógiákat alkalmazni egy-egy jelenség tárgyalásakor. Sőt, akár a diákok is találjanak ki analógiákat. Ezek megbeszélésekor a tanár számára megmutatkozhat az is, hogy mely részeket nem értenek a gyerekek, illetve hol vannak alapvető félreértelmezések.
A diákok számára érdekes feladatot jelent az, ha a különböző összehasonlításokat kell tenniük, mint:
A meglévő tudás és a problémaszituáció közötti kapcsolat felismerése és a tudástranszfer létrejötte szempontjából alapvetően fontos szerepet játszik az analógiás gondolkodás. Az analógiás transzfer alkalmazásához érdekes a következő feladat. <>/P>
Mekkora sebességgel érkezett az elektron a s1 = 20 cm hosszú síkkondenzátor lemezei közé, azokkal párhuzamosan, ha az E = 104 V/m térerősség hatására a kondenzátoron való áthaladás után eltérése az eredeti irányától s2 = 5 cm.
Megoldás: az elektron a beérkezési sebességével megegyező egyenes vonalú egyenletes mozgást végez a kondenzátorlemezekkel párhuzamosan, míg arra merőlegesen egyenletesen gyorsul. A mozgás teljes mértékben hasonló a vízszintes hajításhoz. Az elektron addig az időtartamig, míg s1 = 20 cm = 0,2 m-t megtesz, addig s2 = 5 cm = 0,05 m-t egyenletesen gyorsulva tesz meg. Az elektron gyorsulása: E · e = me · a, innen
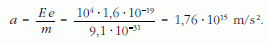
Az egyenletes mozgás ideje: t = s1/v. A gyorsuló mozgással megtett út:
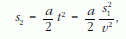
ahonnan e keresett sebesség kifejezhető:

innen a sebesség v = 2,6 · 107 m/s.
A feladat nehézsége abban áll, hogy a fizika tantárgyon belül két különböző területen - a mechanikában és az elektromosságtanban - tanult fogalmakat kell alkalmazni a feladat megoldása során. Az elektron mozgása a kondenzátorlemezben teljesen hasonló (analóg) a vízszintesen elhajított test mozgásához. Csak nem a gravitációs mező, hanem az elektromos mező gyorsítja az elektront a kondenzátor belsejében. Tehát nemcsak a szükséges mechanikai és elektromosságtani ismeretekre van szükség a megoldáshoz, hanem e két terület összekapcsolására is. Továbbá fel kell ismerni a vízszintes hajítással való analógiát, tehát képesnek kell lenni egy analógiás transzferre. Ez csak keveseknek sikerül.
2006-ban a felvett 127 fő elsőéves fizika BSc-s hallgató 25%-a tudta csak megoldani a feladatot. 17 fő megoldása volt teljesen hibátlan. (Az elsőéves BSc-re felvett hallgatók által megírt feladatlap kiértékelésével kapcsolatos részletesebb adatok honlapomon megtalálhatók.) A hallgatókkal megíratott feladatlap megoldásának többi részét kódoló adatok összevetéséből egyértelműen látható, hogy a feladatot a felvettek azon kis százaléka tudta csak jó teljesítménnyel megoldani, akik a feladatlap többi részét is jól oldották meg, tehát komoly tudással is rendelkeztek. Akik csak mechanikából voltak jók, azoknak nem ment a feladat megoldása.
Három kiadó (Nemzeti Tankönyvkiadó, MOZAIK Oktatási Stúdió és Műszaki Kiadó) fizika tankönyvsorozatának a modern fizikával (atomfizika, magfizika, csillagászat) foglalkozó fejezeteit hasonlítottuk össze az analógiák száma szerint. Elsősorban a napjainkban, illetve a közelmúltban forgalomban lévő, és a tanítási gyakorlatban alkalmazott tankönyvek vizsgálatát tűztük ki célul, és mintegy összehasonlításként megnéztünk egy réginek mondható, több, mint 30 éves tankönyvet is (2. táblázat).
A vizsgálatba bevont tankönyvek közül kiemelkedően sok és jó analógia található a Műszaki Kiadó [4] tankönyvében. Ezek nagy mértékben segítik a tananyag megértését, amely a modern fizika alapvetően elvont jellege miatt különösen fontos. A szerzők sok olyan analóg gondolatmenetet is bemutatnak, amelyek ténylegesen elvezettek egy adott felfedezéshez, amelyek fontosak a tudományról alkotott kép, a tudósok munkájának, a fizikai megismerés módszerének bemutatásához is. Ebben a Műszaki Kiadó gondozásában megjelent tankönyv az élen jár. Sok kiváló, szemléletes analógiát mutatnak be az egyébként nehezen elképzelhető jelenségek megértéséhez. Néhány, az analógiás gondolkodást elősegítő feladattal is találkoztunk a könyvekben, aminek nagy szerepe van a gondolkodás fejlesztésében, de ezek száma sajnos igen csekély. Továbbá sajnálatos az, hogy a nukleáris láncreakció és a gyökös mechanizmusú kémiai láncreakciók (pl. égés, HCl szintézise stb.) közti analógiát egyik tankönyv sem alkalmazta. Pedig ez kémiából tananyag a 10. évfolyamon, továbbá tudománytörténeti jelentősége is van, hiszen Szilárd Leó éppen ezt az analógiát használta, amikor kigondolta, hogy érdemes a nukleáris láncreakció kutatásával foglalkozni, és ehhez éppen a kémikusok segítségét kérte és kapta meg a fent említett analógiára hivatkozva.
Írásunk befejező részében a fent említett tankönyvekből mutatunk be néhány érdekes analógiát, amelyeket ajánlunk a majdani tankönyvek írói számára is. A MOZAIK Kiadó [5] tankönyvében a 112. oldalon található kis "történet" szemlélteti a modell és a valóság viszonyát, miszerint a modell soha nem lehet a valóság tökéletes mása. "Képzeljünk el olyan értelmes lényeket, akik mindig csak síkidomokkal találkoztak (kör, téglalap, trapéz stb.). Egyszer lehetőségük adódik, hogy körhengerről készítsenek felvételeket. Ugyanazt a körhengert elölről téglalapnak, felülről körnek látják."
A 130. oldalon szemléletes hasonlatot mutatnak be a képen az atom és az atommag méretviszonyaira, miszerint ha az atommag egy stadion közepére helyezett meggy lenne, akkor az elektronpályák a stadion lelátóira esnének.
A Műszaki Kiadó [4] tankönyvében sok és érdekes analógia olvasható. A 105-106. oldalakon az elektronmikroszkóp működési elvét írják le, amelynek kapcsán összehasonlítják a fényt és az elektront. "A fénysugarak és az elektronpályák közötti analógia mélyebb értelmű. A geometriai optika, amelyben kiterjedten használjuk a fénysugár fogalmát, az általánosabb hullámmodell közelítő leírásának felel meg. A fénysugarakat használó geometriai optika akkor képes megfelelően leírni a fénytani jelenségeket, ha az interferenciával járó jelenségek elhanyagolhatók. Hasonló módon azt is modellnek tekinthetjük, amikor az elektront pontszerű részecskeként kezeljük, amely egy vonallal jellemezhető pályán mozog. Ez a modell akkor alkalmazható, ha az elektronok hullámtermészetével kapcsolatos hatások elhanyagolhatók."
Majd leírják, hogy az elektronmikroszkóp esetében nincs szerepe az elektron hullámtulajdonságainak, a klasszikus newtoni mechanika törvényeit lehet alkalmazni. Szintén analógiaként bemutatják, hogy miként működik az elektrosztatikus lencse és a fénytani lencse.
A 112. oldalon négy kiváló analógiás feladat található. Azonos sebességű proton és elektron hullámhosszát, majd azonos mozgási energiájú proton és elektron hullámhosszát kell kiszámítani és összehasonlítani. Továbbá a Compton-effektust és a fényelektromos hatást, valamint az elektronmikroszkópot és a fénymikroszkópot kell összehasonlítani.
A 126. oldalon az elektronspin szemléltetéséhez az elektron atombeli mozgását a Föld Nap körüli mozgásával és saját tengelye körüli forgásával hasonlítják össze. De ugyanakkor bemutatják az analógia korlátait is, hiszen nem szabad elfeledkezni az elektron hullámszerű viselkedéséről sem. Kifejezetten érdekesek a 127. oldalon leírtak, miszerint az elektron saját mágneses nyomatékának viszonylagos nagy voltára nem tudnak analógiát mondani. Fontos egy ilyen tény hangsúlyozása is, amely esetünkben arra világít rá, hogy a mikrovilág más, mint a makrovilág!
Kifejezetten szellemes a 129. oldalon található hasonlat az adott tulajdonságokkal rendelkező anyagok tervezése és a ruhatervezés között.
Szintén nagyon szellemes hasonlat olvasható a 138. oldalon, ahol a szilárd kristályos anyagokban előforduló diszlokáció mozgását hasonlítják a szerzők egy szőnyegen végigfutó dudorhoz.
A 139. oldalon pedig a szilárd testek sávszerkezeti modelljét szemléltetik, miszerint az elektron vezetési sávba jutását hasonlítják össze egy teli garázsban mozgásképtelen autóval, amely ha fel tudna ugrani a következő üres emeletre, akkor már mehetne is.
A Nemzeti Tankönyvkiadó [6] tankönyvéből egyetlen analógiát mutatunk be. A 93. oldalon az atomban kötött elektron leírásához kétféle modellt mutat be a szerző az Olvasnivaló című részben. Az egyik elképzelés szerint az elektron körpályákon mozgó részecskeként képzelhető el, a másikban állóhullámként.
Néhány nagyon érdekes összehasonlítás és analógia található a régi, Tankönyvkiadó által kiadott tankönyvben is [7].
A 124. oldal két feladatában, (a 2. és a 3.) összehasonlítást kérnek a tanulóktól. Az elektrolitok és a fémek vezetését, illetve a gázok és a félvezetők vezetését kell összehasonlítani.
A 260. oldal közepén az apróbetűs részben egy szilárd anyag atommagjainak egymástól való távolságát érzékeltetik a szerzők, miszerint ha az atommag gombostűfejnyi volna, akkor a szomszédos mag tőle 30 m-re lenne.
A 292. oldalon a magerőt hasonlítják össze a szerzők a Coulomb-erővel és a gravitációs erővel.