Fizikai Szemle honlap |
Tartalomjegyzék |
Laczik Bálint
BME Gyártástudomány és -technológia Tanszék
Lakos Péter
Gravitás 2000 Kft
A kör négyszögesítése az eleve kilátástalan törekvés szinonimája. Kissé tárgyszerűbben: a klasszikus körzős-vonalzós (euklideszi) szerkesztésekkel nem állítható elő olyan négyzet, amelynek területe, avagy kerülete egy adott kör területével (kerületével) egyezik.
Tehát egy tetszőleges körívvel egyező hosszúságú egyenes szakasz sem szerkeszthető.
Az elvi korlátokba ütköző, többé-kevés közismert szerkesztési feladatok nagyrészt az antik görög geometriából származnak. A szögharmadolás, kockakettőzés stb. feladatok azonban valamilyen különleges geometriai eszköz segítségével megoldhatók.
A magyar matematikai irodalom gyöngyszeme, Szőkefalvi Nagy Gyula A geometriai szerkesztések elmélete című kötete (Akadémiai Kiadó, Bp., 1968) nagyszerű bevezetést ad e tárgykörbe.
Az euklideszi eszközökkel nem szerkeszthetőség szabatos bizonyításai mellett különösen érdekesek a feladatok megoldását más úton biztosító, különleges vonalzók és csuklós mechanizmusok.
A matematikatörténet méltatlanul feledett tudósa, Sipos Pál (1759-1816) kochleoid vonalzója1 a körív "kiegyenesítésének" (rektifikálásának) igen ötletes eszköze.
Sipos Pál életútját és munkásságát az [1-4] források részletesen ismertetik. A kochleoid görbe rövid leírása az [5], a jelen cikkhez kapcsolódó, működő Maple worksheet a [6] Internet-oldalon található.
A k paraméterű kochleoidot2 azon k = AP0 hosszúságú körívek P0, …, Pi, …, Pm, … végpontjai alkotják, amelyek közös kezdőpontja A, és az A pontbeli közös érintőjük az A és P0 pontokra fektetett egyenes (1. ábra).
Az AP ív középpontja O, sugara OA = OP = R. Jelölje φ az A csúcsú, a P és P0 pontokon átmenő szárakkal definiált szöget. Az AP húr hossza a húr Q felezőpontjával szerkesztett AQO és QPO (az OQ egyenesre tükörszimmetrikus) derékszögű háromszögek alapján AP = 2Rsinφ. (Az O csúcspontú, az A és Q pontokon átmenő szárakkal definiált szög - a megfelelő szögszárak merőlegessége okán - nyilvánvalóan φ.)
Az AP ív hossza 2Rφ = k, azaz
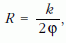
tehát az AP húr hossza
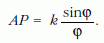
Az R → ∞ ív határalakzata a k hosszúságú AP0 szakasz, a P → A határalakzat az
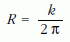
sugarú (az 1. ábrán h-val jelölt, Oh középpontú) kör.
Az O középpontú AB körív hosszával megegyező AT szakasz szerkesztése a 2. ábra szerint történik.
Az AT távolság éppen az AB körív keresett hosszával egyezik meg.
A szerkesztés helyessége könnyen igazolható.
Az AB körív O középpontjából az AB húrra állított merőleges a húrt a Q pontban metszi. Az OQ szakasz az AB ív középponti szögét felezi. Az AB ív középponti szöge 2φ, hiszen a kör OA sugara merőleges az AT egyenesre, az AB húr pedig OQ-ra.
Az AQ = QB fél húrhossz az AQO (avagy a tükörszimmetrikus QBO) derékszögű háromszögekből AQ= QB = Rsinφ, a teljes húrhossz tehát AB = 2Rsinφ.
A kochleoid AP sugara
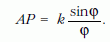
Az A csúcspontú, AP, illetve AT szárakkal adódó φ szöget a párhuzamos AS és BT szakaszokkal metszve az
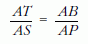
arány adódik, tehát
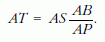
Figyelembe véve, hogy AS = k, AT = 2Rφ éppen az R sugarú, 2φ középponti szögű körív elvileg pontos hossza.
Sipos Pál a kochleoiddal végezhető szerkesztést is tárgyaló dolgozatát 1795-ben a Berlini Tudományos Akadémia aranyéremmel díjazta. Sipos 1796-ban a Bécsben megjelenő Magyar Hírmondóban közreadott hirdetéssel matematikai instrumentuma megvásárlására előfizetőket próbált gyűjteni. A kochleoid vonalzók (az egykorú szöveg szerint) "…egyforma magassággal fognak készíttetni rézből, és mindegyik külön-külön kapsulában lészen; a nyomtatásban kiadandó magyarázat vagy utasítás is mindegyik mellé lesz adva német nyelven. Egy darabnak a hozzá tartozó készülettel együtt az ára tétetett 4 forint 30 krajtzárra."
Sajnos - megannyi kutatás ellenére - sem sikerült kideríteni, egyáltalán készültek-e vonalzók?
A Budapesti Műszaki és Gazdaságtudományi Egyetem Gyártástudomány és -technológia Tanszékén elkészítettük a kochleoid vonalzó néhány mintapéldányát.
A kézi szerkesztési pontosság (~0,03 mm) biztosításához a kochleoidpontok alkalmas száma szükséges.
A görbe

polár egyenletéből képzett
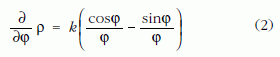
deriválttal a görbe ívhossza a 0 ≤ φ ≤ π tartományban.
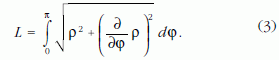
A k = AS = 140 mm értéket felvéve, a (3) ívhossz L = 316,9842432 mm, n = 10 000 görbepontra a szomszédos pontok közötti
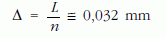
állandó ívtávolság adódik.
Az egyenletes távolságokban felvett görbepontok koordinátáit a &delta1, &delta2, …, &deltai, …, &deltan szögparamétereknél határoztuk meg, ahol a &deltai értékek (i = 1, 2, …, n) az
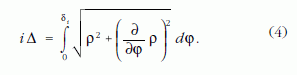
alakú egyenletek numerikus megoldásai. A pontok Descartes-koordinátái:
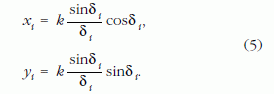
A kochleoid görbe 10 000 pontjának koordinátáit a Maple 12 szimbolikus matematikai rendszerrel számítottuk, majd az alakzat pontláncát DXF formátumban állítottuk elő. A megmunkálás CNC-programját a Mastercam X2-es CAM-rendszer segítségével készítettük el (3. ábra).
Aligha remélhetjük, hogy a geometria oktatásához nélkülözhetetlen lesz e kedves kis eszköz. Úgy érezzük azonban, hogy elkészítésével és elméleti hátterének közreadásával múltunk egy méltatlanul feledett tudós nagysága előtt tiszteleghetünk.
______________________________