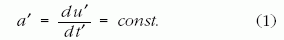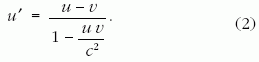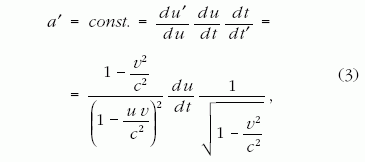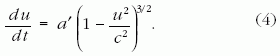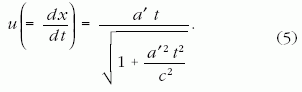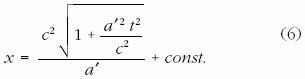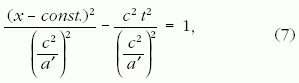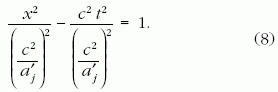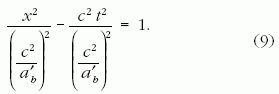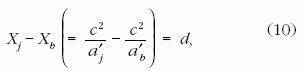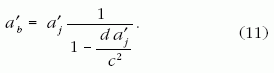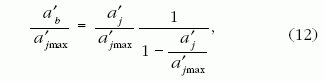RELATIVISZTIKUS FOGÓCSKA - I. RÉSZ

Bokor Nándor
BME Fizika Tanszék

Három, meglepő eredménnyel járó gondolatkísérlet

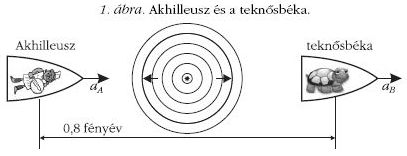
1. Üldözéses versenyhez készülődik a világűrben Akhilleusz és egy teknősbéka. Elhelyezkednek egymástól 0,8 fényév távolságra szabadon lebegő űrhajójukban, ahogy az 1. ábra mutatja. A félúton levő versenybíró fényimpulzussal adja meg a jelet az indulásra. A teknősbéka jobbra indul, Akhilleusz feladata, hogy utolérje.

   A teknősbéka nem ambiciózus, inkább a kényelmet választja. Pontosan földi körülményeket akar teremteni a fedélzeten, ezért állandó a_B = g = 10 m/s² (saját)-gyorsulásra állítja űrhajóját. Akhilleuszban erősebb a versenyszellem, nagyobb, a_A (> a_B) gyorsulással iramodik a teknős után, és - hiába bizonygat Zénón mást - hamarosan utol is éri.

   A verseny visszavágóján megint az 1. ábra szerint helyezkednek el. Ismét egyszerre kapják meg az indítójelet, de a teknősbéka most kicsit jobban rákapcsol. Ismét állandó (saját)gyorsulásra állítja űrhajóját, de most a_B = 1,5 g = 15 m/s² számértékűre. Ezzel a verseny el is dőlt. Akhilleusznak, akárhogyan igyekszik is, elvi esélye sincs, hogy utolérje a teknőst. Hogyan lehetséges ez?

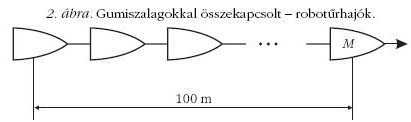
2. Galaktikus távolságokra - gumiszalagokkal összekapcsoltrobotűrhajókból álló konvoj szállítja a teherrakományokat a 2. ábra szerinti elrendezésben. Ezeket a robotűrhajókat úgy tervezték, hogy tetszőlegesen nagy gyorsulást kibírnak, és motorjuk képes is tetszőlegesen nagy gyorsulású mozgásra bírni őket (gondolatkísérlet!). Egyetlen korlátozó tényező van: a konvoj első tagja, a 2. ábrán M-mel jelölt "mozdony"-űrhajó olyan érzékeny vezérlőegységet szállít, amely "csupán" 10¹⁵ m/s² gyorsulást bír ki. A konvoj hossza 100 méter. Az egyes robotűrhajók mozgását úgy hangolják össze, hogy az összekapcsolásukhoz használt gumiszalagok útközben még éppen ne feszüljenek meg.

   A Galaktikus Szállítóvállalat diszpécsere két meglepő tényt jegyez fel:

   1. ) Ha az M űrhajó a benne levő vezérlőegység által még épp kibírható 10¹⁵ m/s² gyorsulással indul, akkor a robotűrhajók közötti gumiszalagok elkerülhetetlenül megnyúlnak.
   2. ) 100 helyett 90 méteres konvojt alkalmazva már nincsen gond: megoldható, hogy a gumiszalagok lazák maradjanak. Hogyan lehetséges ez?
   
   
3. Egy szállítóvállalat pilótái azt a feladatot kapják, hogy egy törékeny anyagból készült "fényévrudat" (ami olyan, mint a méterrúd, csak hossza 1 fényév) a Tejútrendszerből egy másik galaxisba szállítsák. A fényévrúd mentén sűrűn űrhajókat helyeznek el, amelyekhez a rudat rögzítik. Az űrhajókba pilóták ülnek, és várják az indulást. A megbeszélt indulási időpontban egy előzetesen betáplált program szerint az összes űrhajó állandó gyorsulással mozgásba lendül. Az űrhajók mozgása gondosan úgy van összehangolva, hogy szállítás közben a törékeny fényévrúdban se húzó-, se nyomófeszültség ne ébredjen.

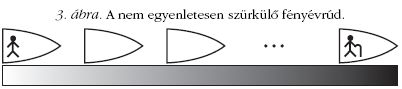
   A fényévrúd speciális festékkel van bevonva: ez induláskor még fehér színű, de az idő múlásával megszürkül, majd teljesen befeketedik.

   Az űrhajók pilótái - akik oldalra kinézve ellenőrzik a hozzájuk képest álló fényévrúd hozzájuk közel eső darabkájának állapotát - érdekes jelenségre lesznek figyelmesek. Mindegyikük azt tapasztalja, hogy a fényévrúd nem egyenletesen szürkül. Minden fényévrúddarab menetirány szerinti hátulja világosabb, mint az eleje (ahogy a 3. ábra mutatja), ami azt jelenti, hogy a fényévrúd egyes darabjai - és így a pilóták - nem azonos ütemben öregednek. Hogyan lehetséges ez?

A Dewan-Beran gondolatkísérlet

Mindhárom fenti példa tág értelemben az úgynevezett Dewan-Beran gondolatkísérlethez [1] (közismertebb, bár kevésbé jogos nevén a "Bell-féle rakétaparadoxon"-hoz) kapcsolódik.

A Dewan-Beran gondolatkísérlet így hangzik:

Két teljesen azonos űrhajót d hosszúságú vékony cérnával kötünk össze. Az űrhajók kezdetben állnak a K inerciarendszerben, ahogy a 4. ábra mutatja. Egyszerre elindulnak (az ábrán jobbra), és teljesen azonos mozgással felgyorsulnak v végsebességre.

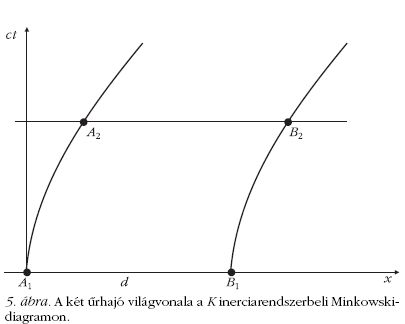
A "teljesen azonos mozgás" azt jelenti, hogy a gyorsulási szakaszaik pontosan ugyanakkora sebességnövekményekből állnak, és ezekre a sebességnövekményekre - akár a K inerciarendszer koordinátaidejét, akár az űrhajósok karóráján mutatott sajátidőt nézzük mindig ugyanazokban az időpontokban tesznek szert. A két űrhajó világvonalát a K inerciarendszerbeli Minkowski-diagramon (5. ábra) ábrázolva az "azonos mozgások" fogalma még könnyebben érthető: a világvonalak azonos alakú görbék, egymásnak pusztán az x-tengely mentén eltolt másai (és kezdeti meredekségük végtelen).

Mi történik a cérnával? A cérna két vége pontosan ugyanazt a mozgást végzi. Azt várnánk tehát, hogy a cérna egésze - anélkül hogy mechanikai feszültség ébredne benne - háborítatlanul mozog jobbra. Azonban ez lehetetlen. Az egyre gyorsabban mozgó cérna hossza ugyanis csak a K inerciarendszerből nézve marad állandó (az 5. ábrán: például A₁B₁ = A₂B₂  = d). Ez viszont - a hosszúságkontrakciót és a cérna egyre gyorsuló mozgását figyelembe véve - azt kell hogy jelentse, hogy a cérna sajáthossza folyamatosan nő. Ez természetesen mechanikai feszültségek létrejöttével is jár, tehát a cérna előbb-utóbb elszakad. A 5. ábra Minkowski-diagramja egyszerű, azonnal átlátható módon írja le a jelenséget, amely azonban így is bántóan ellentmond az intuíciónknak, hiszen a következő mondat igazságát vagyunk kénytelenek megemészteni: "Ha egy éppen csak megfeszített cérna két végét - a cérna hossza mentén - pontosan ugyanolyan módon gyorsítjuk, a cérna előbb-utóbb menthetetlenül elszakad."

A Dewan-Beran gondolatkísérlet által bemutatott jelenségnek nem dinamikai okai vannak. A cérna elszakadását a hosszúságkontrakció tisztán téridő-geometriai effektusa okozza, aminek a newtoni mechanikában nyoma sincs. A gondolatkísérlet arra hívja fel a figyelmet, hogy a hosszúságkontrakció nem csupán a mozgási hossz mérésének módszeréből adódó "illúzió", hanem olyan effektus, amelynek nagyon is valódi (fizikai) következményei lehetnek.

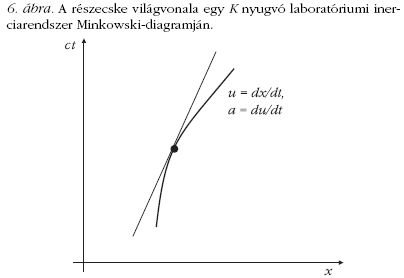
Mielőtt a cikk elején szerepelt gondolatkísérletek meglepő eredményeinek részletes magyarázatába kezdenék, teszek egy olyan feltevést, amely lényegesen egyszerűsíteni fogja a matematikai részleteket: mostantól olyan mozgásokat fogok tekinteni, amelyekben az adott tömegpont sajátgyorsulása állandó. Az első kérdés: milyen görbe írja le az ilyen részecskék világvonalát egy K nyugvó laboratóriumi inerciarendszer (x, ct ) Minkowski-diagramján (6. ábra)?

Állandó sajátgyorsulással mozgó tömegpont

A sajátgyorsulás állandóságát az

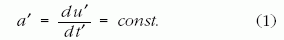
egyenlet fejezi ki, ahol a' a gyorsulás, u' a sebesség (1) és t' az idő. Minden vesszős mennyiség a tömegpont pillanatnyi nyugalmi rendszerében értendő (abban a K' inerciarendszerben, amely olyan v sebességgel mozog a K-hoz képest, hogy O' origója az adott időpillanat kis környezetében éppen együtt mozog a tömegponttal).

A K és K' közötti Lorentz-féle sebességtranszformációs formula:

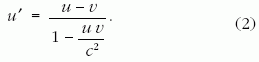
(Azon esemény szűk környezetében tehát, amelyre az (1) egyenletet felírtuk, u = v és u' =0.)

Az (1) egyenletben szereplő deriválást az összetett függvény deriválási szabályával felírva:

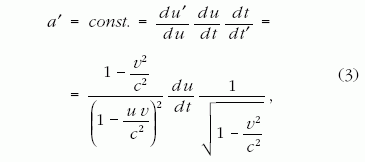
ahol az első tényezőt a (2) egyenlet u szerinti deriválásából kaptuk, a harmadikat pedig az idődilatációs tényezőből. A (3) egyenletet átrendezve, az u = v öszszefüggés felhasználásával a gyorsulásdeficitet kifejező alábbi differenciálegyenlethez jutunk:

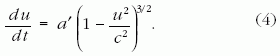
(A gyorsulásdeficit elnevezés abból ered, hogy - mint a (4) egyenlet mutatja - a tömegpont K vonatkoztatási rendszerben mért gyorsulása kisebb, mint a newtoni fizika alapján várt a'.) Az egyenlet közvetlen integrálással kapható megoldása (u(t=0) = 0 kezdőfeltétel mellett, azaz nyugalomból induló tömegpont esetén):

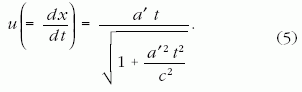
(5)-ből újbóli integrálással megkapható a világvonal alakját leíró x(t) függvény:

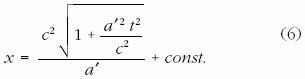
Átrendezés után:

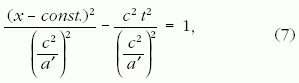
a világvonal alakja tehát hiperbola. A 7. ábra a (7) egyenlettel felírt hiperbolát (illetve annak pozitív a' sajátgyorsuláshoz tartozó ágát) ábrázolja.

Utolérési limit - az 1. gondolatkísérlet magyarázata

A (7) egyenlet alapján könnyű belátni, hogy a hiperbola aszimptotája - mint a 7. ábra is mutatja - azon fénysugár világvonala, amely átmegy a C eseményen (az ábrán a C pont a hiperbola úgynevezett középpontja). Más megfogalmazásban az aszimptota nem más, mint a C eseménynél jelen levő objektumok jövőbeli fénykúpjának jobb oldali "ága". A C-nél jelen levő objektumok tehát - bár kezdetben véges távolságra voltak a tömegpontunktól - soha nem találkozhatnak vele, hiszen világvonaluk - akármennyire is (legfeljebb 45°-kal) dől a ct-tengelyhez képest - soha nem metszheti a (7) hiperbolát.

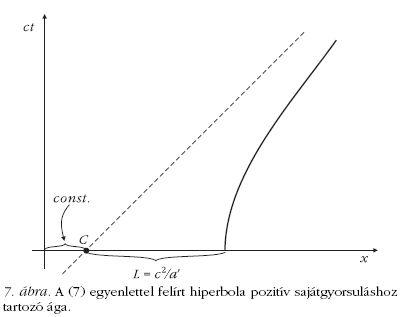
A (7) egyenlet nevezőiben szereplő, hosszúságdimenziójú L = c²/a' kifejezés ennek megfelelően fontos fizikai jelentéssel bír: egyfajta utolérési limitnek tekinthető. Ha egy üldöző űrhajó a t = 0 pillanatban legalább L távolságra helyezkedett el az álló tömegponttól a negatív x-tengely mentén, akkor a tömegpont mozgását leíró hiperbola mindvégig kívül marad az üldöző űrhajó t = 0-beli fénykúpján, azon a tartományon, ahová az üldöző valaha is eljuthat.

A jelenség szépségét az adja, hogy az űrhajók véges távolságból vesznek üldözőbe egy véges sajátgyorsulással mozgó tárgyat, és akármilyen gyorsulással is erednek a nyomába, eleve esélytelenek. Ezzel a cikk elején szereplő 1. gondolatkísérlet meglepő eredménye is érthetővé válik. A számadatok ellenőrzését az olvasóra bízom. (Az a tény, hogy a tömegpont világvonala kívül marad a C-ből kiinduló fénykúpon, természetesen azt is jelenti, hogy még az üldöző űrhajókból kibocsátott fényjelek sem tudják a tömegpontot soha utolérni. Az 1. gondolatkísérletben tehát ha a teknősbéka a_B = 1,5 g értékűre állítja gyorsulását, nemcsak a versenyt sikerül megnyernie, de akkor sem lesz semmi baja, ha a frusztrált Akhilleusz esetleg lézerfegyverrel lő utána.)

A gyorsulás felső korlátja

Mozgassuk a Dewan-Beran-kísérlet cérnájának jobb oldali végét állandó a'_j sajátgyorsulással jobbra. Világvonalát a 8. ábra j jelű hiperbolája mutatja, amelynek az egyenlete:

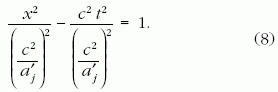
Mint látható, az egyszerűség kedvéért a hiperbolát (8) vízszintes irányban úgy pozicionáltam, hogy az aszimptotája átmenjen az origón. Ez a (7) egyenletben a const. = 0 választásnak felel meg, vagyis annak, hogy a 7. ábra C eseményét (a hiperbola középpontját) az origóba helyeztem.

Mekkora gyorsulással kell mozgatnunk a bal oldali véget, hogy a cérna mindvégig éppen megfeszített maradjon, de ne szakadjon el?

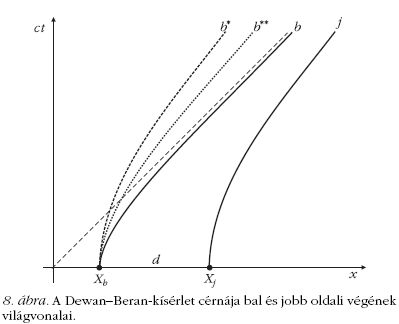
A 8. ábra szaggatottan jelzett b* világvonala, amely a j világvonal eltolt mása, tehát szintén a'_j gyorsulású mozgást ír le, biztosan nem jó: a cérna az ilyen mozgás során elszakad (sajáthossza nő), ezt láttuk már az 5. ábrával kapcsolatban. Hogy a cérna ne szakadjon el, a bal oldali végének nem elég ugyanolyan sajátgyorsulással mozognia, mint a jobb oldali végének, hanem szaporábban kell a jobb oldali vég után igyekeznie. Ilyen lehetséges mozgásokat mutatnak például a 8. ábrán a b** és b jelű világvonalak. Melyik lesz az ilyen mozgások közül a megfelelő?

Próbáljuk ki azt az a'_b állandó sajátgyorsulású mozgást, amelynek egyenlete

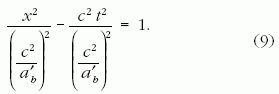
Ez éppen a 8. ábra b-vel jelölt hiperbolája. A (9) egyenletet a (7) egyenlettel összevetve látható ugyanis, hogy ezen eset különlegessége ismét a const. = 0 választás, amely biztosítja, hogy a j jelű hiperboláéval azonos az aszimptotája. Ez, valamint az a követelmény, hogy a két hiperbola kezdeti távolsága az x-tengely mentén legyen d (a cérna kezdeti hossza), egyértelműen meghatározza a'_b értékét:

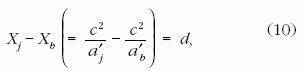
amiből

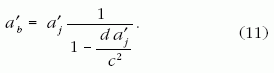
Állítás: ha a bal oldali vég a (11) képletnek megfelelően gyorsul - azaz a b jelű világvonalon mozog -, akkor a cérna sajáthossza (és így megfeszítettségi állapota) mindvégig változatlan marad. Ez az alábbi gondolatmenettel látható be.

A b jelű hiperbola nem más, mint a különböző jobbra mozgó K', K" stb. inerciarendszerek x', x" stb. tengelyeinek kalibrálására szolgáló úgynevezett kalibrációs hiperbola: ez metszené ki az x', x" stb. tengelyekből azt az osztást, ahová a c²/a'_b hosszértéket fel kell mérni. (A (9) hiperbolának ez a tulajdonságaamelynek analógiája az euklideszi síkon az (x, y) derékszögű koordinátarendszerhez képest elforgatott (x', y') tengelyek kalibrálására szolgáló kalibrációs kör - a Minkowski-koordinátákban felírt téridő-intervallum invarianciájából, az x² - c² t² = x'² - c²t'²= … = const. összefüggésből következik). A b világvonalat követő részecske tehát mozgása során mindvégig ugyanakkora, c²/a'_b "téridő-intervallumnyira" van az origó-eseménytől. Ez azt is jelenti, hogy a részecske pillanatnyi nyugalmi inerciarendszereibol végigkövetve a mozgást (egy-egy ilyen inerciarendszerben a részecske világvonala a lokális időtengely irányába mutat) a részecske mindig az adott inerciarendszer x-tengelyének c²/a'_b osztású pontjában tartózkodik, és éppen nyugalomban van. Hasonló módon a j világvonalú részecske is mindvégig ugyanakkora, c²/a'_j "téridő-intervallumnyira" van az origó-eseménytől, tehát ő is minden jobbra mozgó inerciarendszer x-tengelyének ugyanazon jelzésű pontjában (a c²/a'_j pontban) tartózkodik - és éppen nyugalomban van! -, amikor az adott inerciarendszer órái 0-t mutatnak. (Az ilyenkor szokásos módon feltettem, hogy az összes inerciarendszer origója a kezdő időpillanatban egybeesik.) Ez viszont azt jelenti, hogy abban az inerciarendszerben, amelyben a bal oldali cérnavég éppen áll, a jobb oldali cérnavég is éppen áll. Ilyen értelemben a két cérnavég közötti távolság - ami ez esetben a cérna sajáthossza, hiszen abban a rendszerben mért hossz, amelyben a cérna végei állnak - nem változik. A cérna nem szakad el, mindvégig ugyanabban a megfeszítettségi állapotban marad.

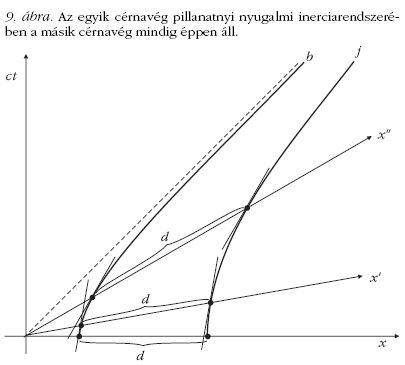
Azt a tényt, hogy az egyik cérnavég pillanatnyi nyugalmi inerciarendszerében a másik cérnavég is mindig éppen áll, a 9. ábra illusztrálja. Az ábrán látható - és analitikusan is könnyen megmutatható -, hogy a két hiperbola meredeksége, azaz a két cérnavég sebessége minden olyan eseménypárban megegyezik, amelyek egy-egy adott inerciarendszer x-tengelye mentén a kezdő időpillanatban egyidejűleg történnek. A két cérnavég tehát egymáshoz képest nem mozog. Érdemes ezt összevetni a b* és j jelű hiperbolák viselkedésével: abban az esetben is kijelenthető, hogy "minden pillanatban megegyezik a két cérnavég sebessége", de ott a "minden pillanatban" szó a végig nyugvó laboratóriumi inerciarendszer egyidejű pillanatait jelenti.

A 8. ábra b és j jelű hiperboláival - (8) és (9) egyenletek - megtaláltuk tehát azt a mozgáspárt, amelyet a cérna bal és jobb oldali végének követnie kell, hogy a cérna mindvégig éppen megfeszített legyen, de ne szakadjon el. (Természetesen a cérna közbülső pontjainak is a megfelelő, egymástól eltérő gyorsulású mozgást kell végezniük. Világvonaluk a 8. ábrán olyan, b és j között elhelyezkedő hiperbolasereget adna, amelyek középpontja az origóban van, és közös aszimptotájuk a 45°-os egyenes.) A fenti számolás bár korrekt - azzal a zavarba ejtő következménnyel jár tehát, hogy a cérna állandó sajáthosszának biztosításához a bal oldali végnek jobban (nagyobb gyorsítóteljesítménnyel) kell igyekeznie, mint a jobb oldali végnek. Ami még zavarbaejtőbb: a jobb oldali cérnavég adott gyorsulású mozgása mellett minél hosszabb a cérna, annál nagyobb gyorsulással kell a bal oldali végnek igyekeznie, hogy a szakadást elkerülje. Felmerül tehát a kérdés: a cérna hosszát növelve nem jutunk-e el előbb-utóbb valamilyen elvi korláthoz, vagyis olyan cérnahosszhoz, amikor a bal oldali cérnavégnek semmilyen mozgása nem tudja a szakadást megakadályozni? Vagy: adott cérnahosszúság mellett a jobb oldali vég sajátgyorsulását növelve nem jutunk-e el előbb-utóbb valamilyen elvi korláthoz, vagyis olyan sajátgyorsuláshoz, amikor a bal oldali végnek semmilyen mozgása nem tudja a cérna szakadását megakadályozni?

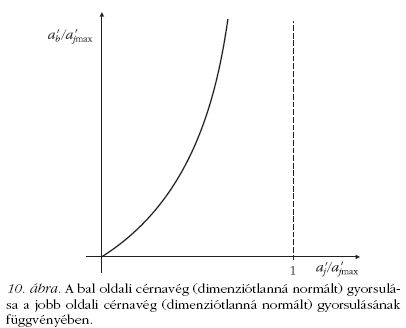
A választ (de igen, vannak ilyen elvi korlátok!) a (11) összefüggésből kiindulva kaphatjuk meg. Sejthető, hogy a képlet jobb oldalán szereplő, gyorsulás dimenziójú c²/d mennyiségnek fontos fizikai tartalma lesz. Vezessük be rá az a'_jmax jelölést (mindjárt kiderül, miért) és a segítségével normáljuk az a'_b és a'_j gyorsulásokat. A (11)-ből így az alábbi dimenziótlan egyenletre jutunk:

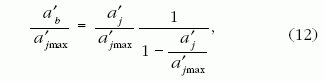
A bal oldali cérnavég (dimenziótlanná normált) gyorsulását a jobb oldali cérnavég (dimenziótlanná normált) gyorsulásának függvényében a 10. ábra mutatja. A (12) egyenletből és a 10. ábrából világossá válik az a?j max konstans jelentése: ahogy a jobb oldali cérnavég gyorsulása megközelíti a'_jmax-ot, a bal oldali cérnavég gyorsulásának végtelenhez kell tartania, hogy a cérna azonos megfeszítettségi állapotban maradhasson. Az

tehát azt a kritikus sajátgyorsulást adja meg, amelyet nem érhet el egy adott d hosszúságú, jobb felé mozgó objektum jobb oldali végének mozgása, ha azt akarjuk, hogy az objektum (ténylegesen, fizikailag) ne nyúljon meg (vagy szakadjon el). Ha a jobb oldali vég a'_jmax-ot elérő vagy meghaladó sajátgyorsulással mozog, akkor a bal oldali végnek még végtelen sajátgyorsulás sem elég ahhoz, hogy "lépést tartson" vele (hogy az objektum sajáthosszát változatlan értéken tartsa).

Irodalom

1. E. Dewan, M. Beran: Note on stress effects due to relativistic contraction. Am. J. Phys. 27 (1959) 517.