AZ ELTŰNT SZIMMETRIA NYOMÁBAN - a 2008.évi fizikai Nobel-díj

Trócsányi Zoltán
Debreceni Egyetem és MTA ATOMKI

Vegyítsed enyvvel, vagy kőporban főzd,
Bocsásd rá sáskák falánk hadát,
Fő elv lebegjen szemed előtt
Ne bontsd meg a szimmetriát!
Lewis Carroll

Szimmetria a szépség alapja

A Lewis Carrolltól származó idézet mutatja, hogy életünkben lényeges szerepet játszanak a szimmetriák. Klasszikus építészek például szimmetrikus épületeket kedveltek tervezni. Nem véletlenül: a szimmetrikus alakzatokat szépnek látjuk. Például a szépségkirálynők arca szinte tökéletes jobb-bal (tükrözés-) szimmetriát mutat, az aszimmetrikus arcokat pedig nem találjuk szépnek (1. ábra). A szimmetrikus alakot tökéletesebbnek gondoljuk, leírásuk egyszerűbb, könnyebben megjegyezhető, mint a kevésbé szimmetrikusé. Például a gömb nagyfokú térbeli szimmetriával rendelkezik, meghatározásához egyetlen adat, a sugara elegendő.

Szimmetria a fizikában

A fizika fejlődése szempontjából lényeges felismerés volt, hogy sok jelenség szimmetrikus valamilyen értelemben, ami erősen megszorítja a jelenséget leíró elmélet alakját. Például, ha filmre vesszük két golyó rugalmas ütközését, majd visszafelé lejátsszuk, akkor semmi különöset nem veszünk észre, ami azt jelenti, hogy a rugalmas ütközésekről szóló emlékeink szerint az időben megfordított ütközés éppen úgy valódinak tűnik, mint az eredeti. Az ütközést leíró törvények változatlanok maradnak az idő megfordításakor (időtükrözés, jele T). Ennek következménye, hogy a két golyó rugalmas ütközését leíró elméletben csak az idő szerinti páros derivált szerepelhet. A Newton-elmélet ezek közül a legegyszerűbbet (az idő szerinti második deriváltat) választja - sikeresen. Az időtükrözés diszkrét transzformáció. Kétszer egymás után alkalmazva az eredeti időirány áll elő, T² = 1.Hozzá hasonló a tértükrözés (jele P, P² = 1). Léteznek folytonos transzformációk is. Például a Newtonelmélet (időtől nem függő kölcsönhatás esetén) az időt csak deriváltként tartalmazza, ezért az időeltolás esetén sem változik, az események ugyanúgy játszódnak le az eltolt időben is. Emmy Noether vette észre, hogy minden folytonos szimmetriához megmaradó mennyiség tartozik. Például térbeli eltolások a Newton-egyenletet nem változtatják meg - az ehhez tartozó megmaradó mennyiség a lendület -, míg a térbeli forgatásokkal szembeni szimmetria következménye a perdület megmaradása. Konzervatív erők esetén a Newton-egyenlet időeltolás esetén sem változik, aminek következménye a mechanikai energia megmaradása. Hendrik Lorentz (Nobel-díj 1902) vette észre, hogy az elektromosság Maxwell-féle elmélete a tér-idő másfajta (Lorentz) transzformációja esetén is változatlan marad, majd Henri Poincaré francia matematikus megmutatta, hogy a tér-idő felsorolt folytonos transzformációi csoportot alkotnak (Poincaré-csoport).

Szimmetria a részecskefizikában¹

A részecskefizika tárgya az anyag alapvető kölcsönhatásainak tanulmányozása. Az említett tér-idő transzformációkkal szembeni szimmetriák erősen megszorítják az elméletek alakját. A négy alapvető kölcsönhatás matematikai leírása szempontjából azonban döntő jelentőségűnek bizonyult Hermann Weyl felismerése, hogy az elektron elektromosságának elmélete olyan szimmetriát mutat, amely nem köthető a tér, vagy az idő transzformációjához. Azt már Weyl előtt is tudták, hogy az elmélet változatlan marad, ha az elektronmező fázisát a tér minden pontjában ugyanannak, de szabadon választjuk meg. Felfogható ez is egyfajta forgásszimmetriának, amelynek a szimmetriacsoportja a kétdimenziós forgatások csoportja, csak ez alkalommal a forgatás egy kétdimenziós vektoron hat, amelynek összetevői az elektronmező valós és képzetes része. Az ilyen, nem a tér-idő transzformációjához, hanem egy fizikai mező transzformációjához köthető szimmetriát belső szimmetriának nevezik. Noether tétele szerint a helytől nem függő (globális) belső transzformációval szembeni szimmetria is megmaradó mennyiséghez - az elektron esetében az elektromos töltés megmaradásához - kapcsolható.

Weyl - saját korában nem kellően értékelt - felfedezése az volt, hogy amennyiben feltételezzük, hogy a belső szimmetria lokális, úgynevezett mértékszimmetria - például az elektronmező fázisa a tér-idő minden pontjában szabadon választható meg -, akkor az elméletben megjelenik egy másik fizikai mező, a mértékmező, amely a részecskék közötti kölcsönhatást közvetíti. Például az elektron esetén a mértékmező az elektromágneses mezővel azonosítható. Ilyen módon a lokális szimmetria egy teljes, az elektron és az elektromágneses mező kölcsönhatását leíró elméletet, az elektrodinamikát eredményezi. A szabad fázisválasztás egységnyi hosszú komplex számmal (e^iφ) való szorzást jelent, ahol a φ fázis a hely függvénye. Az ilyen szorzások unitér csoportot alkotnak.² A csoportelemek felcserélhetőek, ezért a csoport Abel-féle, és az elektrodinamika ábeli mértékelmélet.

A mértékszimmetriánál szebb, gazdaságosabb (kinek- kinek ízlése szerint) elméletépítés nem képzelhető el. Kiindulunk valamely anyagmezőből, feltételezzük, hogy az elmélet mértékszimmetrikus valamely unitér csoport elemeinek transzformációjával szemben, és máris egy teljes, anyag és mértékmező dinamikus kölcsönhatását leíró elméletet kapunk. Ráadásul az ilyen elméletek könnyen, és matematikailag értelmesen kvantálhatók. A kvantálás után kvantummezőelméletet kapunk.A négy alapvető kölcsönhatás közül hármat (az erős, valamint az elektromágneses és a gyenge kölcsönhatásokat egyesítő elektrogyenge kölcsönhatást) kvantum-mezőelméletben ír le a részecskefizika Standard modellje. Az elmélet részletei az irodalomban sok helyen megtalálhatók. Rövid összefoglalást ad például a [3] cikk.

A mértékelméletre alapuló Standard modell a mérési adatok nagypontosságú leírását szolgáltatja. Az elektron-pozitron ütközésekben mérhető mennyiségeknek a Standard modellel számolt, valamint a Nagy Elektron-Pozitron gyorsítónál (LEP) mért értékei közötti egyezés rendkívül meggyőző, ami a Standard modell fizikai helyességét sugallja. A Standard modell szimmetriája azonban közvetlenül nem tapasztalható a valóságban. Tömeggel rendelkező részecskéket leíró elmélet ugyanis nem rendelkezhet a Standard modell szimmetriájával, a tapasztalat szerint azonban az összes anyagmező, továbbá a mértékmezők elemi gerjesztései közül három tömeggel rendelkezik. A mai részecskefizika legfontosabb válaszra váró kérdése, hogy hogyan marad rejtve az elektrogyenge szimmetria, amit úgy is szoktak fogalmazni, "honnan nyerik az elemi részecskék tömegüket?"

Spontán szimmetriasértés

A helyzet meglehetősen ellentmondásos. Egyrészt van egy szimmetriára alapuló modell, amellyel nagy pontossággal lehet mérhető mennyiségekre becslést tenni, és az elméleti számítások igen jól egyeznek a kísérletileg mért értékekkel. Ilyen helyzetben magabiztosan azt szoktuk mondani, hogy az elméleti leírásunk helyes. Másrészt azonban a megfigyelhető részecskék fizikai tulajdonságai egyértelműen sértik a feltételezett szimmetriát, tehát a szimmetriaelvre alapuló leírás nem lehet helyes. Vagy mégis?

A következő részben találkozunk majd olyan jelenséggel, amikor az elmélet valamely transzformáció esetén remélt szimmetriát sért. Az ilyet nevezik dinamikai szimmetriasértésnek.A mértékszimmetria dinamikai sértése azonban (itt nem részletezendő) súlyos elvi problémákat vet fel. Létezik azonban a természetben olyan jelenség is, amikor a természeti törvények szimmetriáját a megfigyelhető jelenségek nem tükrözik. Például egy hegyére állított ceruza forgásszimmetrikus környezetben forgásszimmetrikus egyensúlyi helyzetben van, amely azonban nem marad tartósan fenn (labilis).Bár milyen piciny hatás ki tudja téríteni az egyensúlyi helyzetből és feldől, aminek eredményeként egy olyan alacsonyabb energiájú állapotba kerül, amely az eredetileg meglévő forgásszimmetriát sérti. Ha a ceruza látható külső beavatkozás nélkül feldől, akkor a feldőlt állapotban a szimmetria spontán sérül (2. ábra).

A spontán szimmetriasérülés gyakori jelenség a természetben. Például egy kör alakú terített asztalon egy tányérhoz tartozhat akár a jobbra, akár a balra elhelyezett pohár. Ezt a szimmetriát vagy egyezség alapján sértik meg az asztalnál ülők, vagy valaki spontán módon. Spontán szimmetriasértés hatására nem a rendszer dinamikáját leíró elmélet szimmetriája sérül, csupán a rendszer legalacsonyabb energiájú állapota, az alapállapot sérti meg a szimmetriát.

Hasonló fegyvert vetettek be - bár nem nevezték néven - 1956-ban John Bardeen, Leon Cooper és Robert Schrieffer (Nobel-díj 1972) a szupravezetés elméleti értelmezése érdekében. A szupravezető lényegében egy olyan anyag, amelyben az elektron fázisának szabad megválasztása spontán sérül, csak a fázis 180°-os változtatásával, azaz előjelének ellenkezőjére történő változtatásával szembeni szimmetria marad meg. Az ilyen spontán szimmetriasértés eredményeként páros számú elektron alapállapoti várható értéke nullánál nagyobb, míg egy elektron állapotának várható értéke nulla a szupravezetőben. A szupravezető összes különleges tulajdonsága - például a nulla elektromos ellenállás, a Meissner-hatás, a mágneses fluxus kvantáltsága egy vastag szupravezető gyűrűben - mind következik az elektron fázisválasztási szimmetriájának spontán sérüléséből.

A szupravezetés BCS-elmélete tényleg csak hasonló a spontán szimmetriasértéshez. Modelljükben abból a feltevésből indultak ki, hogy elektronpárok tagjai csak akkor hatnak kölcsön, ha energiájuk egy bizonyos - Fermi-szintnek nevezett - értékhez közeli. Az olvasóban felmerülhet a kérdés, hogyan lehet egy közelítésen alapuló modellel pontosan eltűnő elektromos ellenállást megmagyarázni. A válasz az, hogy pontosan nem. Csak a szimmetriaelvre épülő modell képes pontos magyarázatot szolgáltatni.

Spontán szimmetriasértés a részecskefizikában

Nambu az atommagok béta-bomlásának elmélete kapcsán próbálkozott a spontán szimmetriasértéssel. Az atommagban található neutronnak protonná, elektronná és antineutrínóvá történő bomlásáért a magban fellépő kétféle áram felelős. Az egyik hasonló a szokásos elektromos áramhoz, amennyiben Lorentz-transzformációk esetén úgy viselkedik, mint egy vektor, ezért vektoráramnak nevezik. Ez az áram megmaradó áram, tehát ugyanúgy folytonos szimmetriához tartozik, mint a megmaradó elektromos áram. Már említettük, hogy az utóbbi az elektronmező globális fázisválasztási szimmetriájának következménye, az előbbi pedig a globális izospin szimmetriáé.

A másik áram az axiálvektor-áram.³ Vajon ez is megmaradó áram? Ha igen, akkor ez is folytonos szimmetria következménye. Ilyen szimmetriák lehetnének a királis (jobbkéz-balkéz) szimmetriák, azonban ezek következménye az lenne, hogy vagy a nukleonok tömege nulla - ami nem teljesül -, vagy léteznie kell három nulla tömegű és spinű részecskének, amelynek hullámfüggvénye tértükrözéskor előjelet vált - ami szintén nem teljesül a természetben. Ez a két lehetőség fizikailag annyit jelent, hogy ilyen szimmetria vagy nincs (ezért van a nukleonoknak tömegük), vagy pedig spontán sérül magában az üres térben (ezért kellene nulla tömegű részecskéknek létezni) nem csak anyagban, mint a szupravezetés esetén.

A kiemelkedő kutatóknak két fontos tulajdonsága van. Egyrészt ragaszkodnak a tényekhez, másrészt nem ijednek meg tőlük. Bár Nambu korában is nyilvánvaló volt, hogy ilyen királis szimmetria nem létezhet, mégis feltette, hogy "közelítőleg" létezik, és spontán sérül az üres térben. Pontos szimmetria spontán sérülésekor nulla tömegű részecskének kell lenni. Nambu érvelése szerint közelítő királis szimmetria spontán sérülésekor a nulla spinű részecske tömege csak közelítőleg lesz nulla. Ezt a részecskét Nambu a pionnal azonosította.

Bár az idő nem igazolta Nambu modelljét, azonban övé volt az első bátor próbálkozás, hogy a spontán szimmetriasértést mezőelméleti nyelven is megfogalmazza. Nem sokkal később Jeffrey Goldstone további példákat mutatott a spontán szimmetriasértés mezőelméleti megfogalmazására, és arra, hogy ez mindig nullatömegű részecskék létezését jelenti. Azóta ezeket a részecskéket (Nambu-) Goldstone-bozonoknak hívjuk.

Goldstone-bozont azonban nem sikerült találni a természetben, ami azt jelentette, hogy vagy nem létezik spontán szimmetriasértés a részecskefizikában, vagy valami kiutat kell találni. A kiútra P. Higgs, G. Guralnik, R. Brout és F. Englert, valamint D. Hagen és T. Kibble munkái vezettek, bár manapság leginkább csak Higgs-mechanizmusnak hívjuk. A Goldstone- bozonok megjelenése globális szimmetria spontán sérülésekor történik. A felsorolt kutatók megmutatták, hogyha lokális (mérték-) szimmetria sérül spontán, akkor a Goldstone-bozonok longitudinális polarizációként hozzáadódnak a mértékelmélet mértékmezőinek két transzverzális polarizációs szabadsági fokához, amitől a szimmetrikus elméletben a nullatömegű mértékbozonok tömeget nyernek.⁴ (Képszerűen: a mértékbozonok megeszik a Goldstone- bozonokat, amitől tömegük lesz.)

Az előző szakaszt éppen azzal a problémával kezdtük, hogyan lehet egy mértékszimmetrikus elméletben a részecskéknek tömegük. Erre a Higgs-mechanizmus nagyon szép és gazdaságos - bár nem kizárólagos - lehetőséget nyújt. A jelenség lényegéről, és a hozzá kapcsolódó Higgs-részecske kereséséről korábbi cikkemben már olvashattak a Szemle olvasói [4], ezért itt tovább nem tárgyaljuk. Az LHC gyorsító üzembehelyezésével felfokozódtak a várakozások, hogy sikerül megfigyelni a Higgs-részecskét a laboratóriumban, ami bizony Nobel-díjas felfedezés lenne. Előtte azonban a Nobel-bizottság díjjal kívánta jutalmazni azt az elméleti munkásságot is, amely a spontán szimmetriasértés lehetőségét felvetette az elemi részecskék világában. Ezért kapta Nambu a 2008. évi fizikai Nobel-díj felét.

Diszkrét szimmetriák a részecskefizikában⁵

A részecskefizika fejlődésére döntő hatással volt a diszkrét szimmetriák vizsgálata is. Háromféle diszkrét szimmetriát ismerünk: a már említett idő- és tértükrözést, valamint a töltéstükrözést (jele C, C² = 1). A tértükrözés a térkoordinátákat ellenkező előjelűre változtatja, hatására egy részecske lendülete előjelet vált, spinje (sajátperdülete) azonban változatlan marad. Relativisztikus sebességgel mozgó fermionok ( ħ/2 spinű részecskék) állapotának jellemzéséhez jó kvantumszám a helicitás, ami lényegében a részecske spinjének a lendület irányába eső vetülete. Pozitív helicitású - "jobbkezes", jele R - részecske spinjének és lendületének iránya egybeesik, míg a negatív helicitásúé - "balkezes", jele L - ellentétes. Tértükrözés hatására a helicitás az ellenkezőjére változik: jobbkezesből balkezes lesz és viszont. A töltéstükrözés részecskéhez antirészecskét rendel. Egy részecske antirészecskéjének minden fizikai tulajdonsága ugyanaz, csak az elektromos töltése ellentétes.⁶

A részecskéket piciny golyóknak elképzelve, a newtoni mechanikán nevelkedve, úgy gondolhatjuk, hogy kölcsönhatásuk mind az idő, mind a tértükrözéssel szemben változatlan. Igen nagy volt hát a fizikusközösség meglepetése, amikor Tsung-Dao Lee és Chen-Ning Yang (Nobel-díj 1957) elméleti felvetésére C.S. Wu 1956-ban kimutatta, hogy a gyenge kölcsönhatásban a tértükrözési szimmetria sérül. Wu kísérletéről, valamint a Leon Lederman csoportja (Nobel-díj 1988) által végzett megerősítő kísérletről a közelmúltban részletesen olvashattak a Szemle olvasói [5].

Ledermanék kísérlete egyszerűbben kivitelezhető. Szénben megállított pozitívtöltésű pionok antimüonná és neutrínóvá történő bomlását tanulmányozták. A pion spinje nulla, így a perdület megmaradása szerint a keletkező két részecske spinje ellentétes irányú. A lendületük is az, hiszen az álló pion lendülete is nulla. Ezek szerint mindkét bomlástermék vagy balkezes, vagy jobbkezes. Tapasztalatuk szerint az antimüon mindig balkezes volt (a neutrínót nem lehet észlelni, ezért spinállapotát sem lehet meghatározni). A tapasztalat tehát az, hogy a pozitívpion bomlásakor a jobbkezes neutrínó keletkezéséhez tartozó bomlási szélesség nulla, Γ(π⁺ → μ⁺ ν_R) = 0, míg a balkezeséhez tartozó nagyobb, mint nulla, Γ(π⁺ → μ⁺ ν_L) ≠ 0 A két folyamat tértükrözéssel egymásba vihető, P(π⁺ → μ⁺ ν_L) = (π⁺ → μ⁺ ν_R) így a bomlási szélességek különbözősége a tértükrözés sérülését jelenti. A kísérletet negatív töltésű pionnal elvégezve a töltéstükrözési szimmetriát lehet ellenőrizni. Minthogy a töltéstükrözött folyamat, 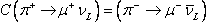bomlási szélessége szintén nulla, 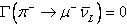, ezért tapasztalat szerint a gyenge kölcsönhatásban a töltéstükrözési szimmetria is sérül! 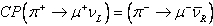Ugyanakkor az egyszerre töltés- és tértükrözött folyamat, , bomlási szélessége ugyanakkora, 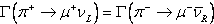, ami azt súgja, hogy a gyenge kölcsönhatás megőrzi a CP-szimmetriát.

A részecskefizikai Standard modellnek létezik egy olyan megfogalmazása, amelyben a folyamatokat gráfokkal írjuk le. A modell építőkövei a fermionok (elektron, müon, tauon és neutrínóik, u, d, s, c, t, b jelű kvarkok), amelyeknek egy irányított folytonos vonal felel meg. A gráfokat balról jobbra olvassuk. Fermionvonalak irányítása jobbra mutat, az antifermionoké balra. A fermionok közötti kölcsönhatást a mértékmezők elemi gerjesztései a spinű bozonok közvetítik. Ide tartozik az elektromágnességet közvetítő foton (γ), amelyet hullámos vonallal, a gyenge kölcsönhatást közvetítő töltött (W^±) és semleges (Z⁰) bozon, amelyeket fűrészvonallal, és az erős kölcsönhatást közvetítő gluon (g), amelyet hurkolt vonallal jelölünk (4. ábra). A részecskék közötti kölcsönhatásnak egy pontban összefutó három vonal felel meg, két fermion- és egy bozonvonal. (Létezik olyan is amikor csak bozonvonalak futnak össze - ilyenkor lehet négy vonal is -, de ez érvelésünk szempontjából nem lesz lényeges.) Az összefutó fermionvonalak irányítása folytonos (egy be- és egy kifutó vonal), tehát egy kölcsönhatásban egy fermion, egy antifermion és egy bozon vesz részt. A számunkra most érdekes néhány kölcsönhatást (szaknyelven áramot) mutat a 4. ábra. A W^±-hoz csatolódó áram töltött, a Z⁰-hoz, vagy fotonhoz, gluonhoz csatolódó áram semleges.

A Richard Feynmanról (Nobel-díj 1965) elnevezett gráfszabályok segítségével a pionbomlásos folyamatokat az 5. ábrán mutatjuk. A fenti érvelésünkből kitűnik, hogy a diszkrét szimmetriák tanulmányozása szempontjából lényeges a részecskék lendületének és spinjének iránya is, ezért a szokásos Feynman-gráfokat kiegészítettük egy ábrával, amelyen a részecskék lendületének (vékony, hosszú nyíl) és spinjének (vastag, rövid nyíl) irányát mutatjuk. Említettük, hogy a piont bomlása előtt megállítjuk, tehát lendülete nulla (pont) és a spinje is az. A lendület és perdület megmaradása szerint a bomlástermékek teljes lendülete és spinje is nulla.

A gyenge kölcsönhatás elméletének születésekor ismert kísérleti tapasztalatok szerint a töltött áramokban résztvevő fermion-antifermion pár a következő párokból állhatott:

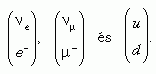
(A felső komponens elektromos töltése pontosan egy protontöltéssel nagyobb az alsó komponens töltésénél, így a töltött áramban szereplő mértékbozon töltése is egységnyi. Semleges áramban nyilván csak ugyanaz a fajta részecske-antirészecske pár szerepelhet.) Ekkor már tudták, hogy létezik egy harmadik, az u-nál és d-nél lényegesen nehezebb kvark is, amelyet s-sel jelöltek. Természetes feltevés volt, hogy ennek is van egy párja, a c-kvark, és a könnyű (elektron) és nehéz (müon) leptoncsaládnak megfelelően van egy könnyű (u, d) és egy nehéz (c, s) kvarkcsalád. Az elképzelés szép, azonban eleve tudták, hogy baj van vele.

Ismerték ugyanis a töltött kaont, amely egy u és egy anti-s kötött állapota, és elbomolhat a K⁺ → µ⁺ν_µ folyamat szerint, tehát léteznie kell olyan töltött gyenge áramnak, amely egy u-t és egy anti-s-t csatol össze (6. ábra). Ez ellentmond a fenti elképzelésnek, amely csak u és d, valamint c és s közötti csatolást enged meg. Újfajta áramok bevezetése helyett Nicola Cabbibo azt javasolta, hogy a töltött áramokban az eredeti d- és s-kvarkok keveréke szerepel:

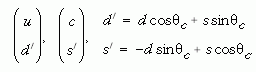
A θ_C keveredési szöget Cabbibo-szögnek nevezik. Így a q₁ és q₂ kvarkok töltött áramában az eredetihez képest megjelenik egy V_{q1 q2} szorzótényező, ahol

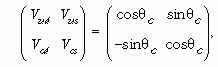
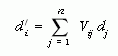
alakban írhatjuk, ahol d_j, illetve d'_j jelölik az n = 2 darab eredeti, illetve kevert alsó kvarkállapotot, és V_ij a keveredést leíró mátrix.

A Cabbibo-szög értéke megmérhető. Vegyük például az s-kvarkszám megváltozásával járó (ΔS = 1) kaon-bomlás, K⁺ → μ⁺ ν_μ, és az s-kvarkszám változásával nem járó (ΔS = 0) pion-bomlás, π⁺ → μ⁺ ν_μ, szélességének hányadosát. A kaon-bomlás amplitúdójában szerepel egy V_us tényező, a pion-bomláséban pedig V_ud. Ettől eltekintve a két folyamat nagyon hasonló. A bomlási szélesség az amplitúdó négyzetével arányos, ezért

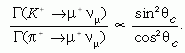
A bomlási szélességek hányadosából tehát a Cabbibo- szög megkapható. Természetesen a Cabbibo-szög más bomlásokban is felmerül. Megnyugtató, hogy értéke minden bomlásban ugyanakkora, tehát a d- és s-kvarkokra vonatkozó keveredést a tapasztalat alátámasztja.

Kísérleti tapasztalat szerint d- és s-kvarkot egyszerre tartalmazó ("ízcserélő") semleges gyenge áram nem létezik (vagy nagyon pici az ilyen áramot tartalmazó bomlás bomlási szélessége). Igen ám, de ha a fizikai alsó (d_i) kvarkállapotok helyett a semleges áramban a kevert alsó (d'_i) kvarkállapotok szerepelnek, akkor elvileg előfordulhat ízcserélő semleges áram. Hogy ez mégse fordulhasson elő, szükséges, hogy a keveredést leíró V mátrix unitér legyen, V⁺ V = 1. Ekkor ugyanis a semleges áramban megjelenő d'-kvark keveredését a V, az anti-d'_i-kvark keveredését pedig a V⁺ mátrix adja, a kettő együttes hatása pedig éppen az egységmátrix. Ha tehát a fizikai d_i-kvarkállapotok esetén nem volt ízcserélő semleges gyenge áram, akkor a kevert d'_i-kvarkállapotok esetén sincs (7. ábra). Ezt az észrevételt, amelyet elsőként S. Glashow, J. Iliopulous és L. Maiani írtak le, nevezik GIM-mechanizmusnak.

Az egyesített CP-szimmetria is sérül!

Említettük, hogy a bomlási szélességekre vonatkozó mérési eredmények azt súgták, hogy a gyenge kölcsönhatásban a CP-szimmetria megmarad. A semleges kaon bomlása remek lehetőséget kínál ennek ellenőrzésére. Semleges kaonból kétféle létezik, 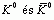. Mindkettő keletkezik pion és proton kemény ütközésekor. Például az előbbi a π^- p → K⁰ Λ⁰ folyamatban (8. ábra), míg az utóbbi a 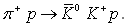folyamatban. Megfigyelések azt sugallják, hogy a K⁰ kaon valójában két részecske, ugyanis vagy viszonylag gyorsan, 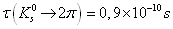alatt elbomlik két semleges pionra, vagy ezerszer lassabban, 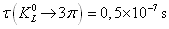alatt háromra. A gyorsan bomló állapot, 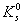együttes tér- és időtükrözés esetén változatlan marad, míg a "hosszú" élettartamú 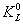állapota előjelet vált, ugyanis egyetlen pion állapota CP-tükrözésre előjelet vált. 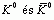Ez a két állapot kikeverhető a állapotokból, ha a kettő közötti relatív fázist úgy választjuk meg, hogy CP .

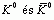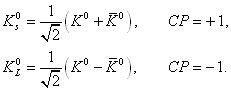
Ez így a jelenségek összecsengő értelmezése. A meglepetés az, hogy ha megfelelő kísérleti összeállításban - amilyet például J. Christenson, J.W. Cronin, V.I. Fitch és R. Turlay készítettek 1964-ben (Nobel-díj: Cronin és Fitch, 1984) - sikerül a rövid és hosszú élettartamú K⁰-t szétválasztani, akkor ritkán (ezer bomlásból kétszer) előfordul, hogy a hosszú élettartamú 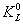mégiscsak két semleges pionba bomlik, amit a CP-szimmetria tiltana, azaz gyenge kölcsönhatásban a CP-szimmetria ha gyengén is, de sérül.

Hogyan értelmezhetjük a CP-szimmetria sérülését?

Csodálatos módon a Standard modell természetes megoldást kínál erre a kérdésre. Ahogy a kvantumelméletben megszoktuk, a modellnek önadjungáltnak kell lenni. A gráfok nyelvére lefordítva ez annyit jelent, hogyha a modell tartalmaz egy folyamatot, akkor tartalmaznia kell az adjungáltját is. Az adjungálás megfordítja a fermionvonulat irányát, és mindent komplex konjugál. Ennek megfelelően például a K⁺ → μ⁺ ν_μ folyamat adjungáltja a 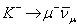folyamat, azzal a kiegészítéssel, hogy az utóbbiban a V_us mátrixelem helyére a komplex konjugáltját kell írni (9. ábra). E két folyamat azonban egymás CP-tükrözöttje is, 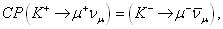, csakhogy CP-tükrözéskor nem kell a V_us mátrixelem komplex konjugáltját venni (10. ábra). Ha a V mátrix valós, akkor az eredeti és a CP-tükrözött elmélet egybeesik (a 9. és 10. ábra ugyanazt a két folyamatot írja le). Ha V komplex, akkor a CP-szimmetria sérül.

A keveredési mátrixról annyit tudunk, hogy unitérnek kell lennie. Egy általános n × n-es unitér mátrixnak n² független paramétere van (2n² paraméter, közöttük n² megszorítással). Ez a mátrix n db felső és n db alsó kvarkállapotot kapcsol össze, amelyek fázisa szabadon választható. Ezek ügyes megválasztásával a V mátrixelemekben található fázisok közül (2n-1) eltüntethető. (Nem 2n, csak (2n-1), mert egyetlen kvark fáziseltolása egyenértékű az összes kvark fázisának ugyanolyan mértékű eltolásával.)

Ha az így kapott mátrix minden eleme valós, akkor n(n-1) / 2 független paramétere van (valós unitér mátrix független elemeinek száma). Ha a független paraméterek száma nagyobb, akkor a mátrix nem lehet valós. Ezek alapján egyszerű számolás szerint a mátrix komplex paramétereinek száma

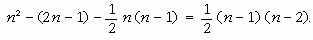
Két kvarkcsalád esetén (n = 2) ez a szám nulla. Három kvarkcsalád esetén azonban egy, tehát ekkor a keveredési mátrix komplex, és a modellben megjelenik a CP-sértés. Ezt az észrevételt elsőként M. Kobayashi és T. Maskawa írta le 1964-ben egy - azóta nagyon híressé vált - rövid cikkben, amiért 2008-ban megosztva kapták a fizikai Nobel-díj másik felét (11. ábra). Azért éppen most, mert ekkorra sikerült sok kísérlettel egyértelműen megmutatni, hogy a természetben található CP-sértő jelenségek mind pontosan leírhatók a Standard modellel. Például a semleges kaonokon kívül csak 2001-ben sikerült egyáltalán kimutatni a CP-sérülését B-mezonok bomlásában.

A Cabbibo-Kobayashi-Maskawa keveredési mátrixban található komplex fázis a CP-sértés kizárólagos oka a Standard modellben. A figyelmes olvasó azonban felvetheti, hogy a bomlási szélességben az amplitúdó abszolút értékének négyzete szerepel, amiből a komplex fázis kiesik; akkor hogyan tud egy komplex fázis mérhető hatást okozni. Nos egy bomlási folyamat nem csak egyféle módon lehetséges. Például a semleges B⁰-mezon bomlása töltött pionpárba a 12. ábrán látható mindkét gráf által mutatott módon történhet.⁷ Mindkét folyamatban megjelenik a komplex fázis, de különböző együtthatókkal, így a teljes amplitúdó szerkezete a+be^iφ alakú, amely abszolút értékének négyzete a²+b²+2abcosφ, tehát már nem esik ki a komplex fázis hatása.

1. Patkós András: A részecskefizika rejtőzködő szimmetriái. Fizikai Szemle 58 (2008) 126.
2. Horváth Dezső: Szimmetriák az elemi részecskék világában. Fizikai Szemle 53 (2003) 122.
3. Horváth Dezső: A részecskefizika anyagelmélete: a Standard modell. Fizikai Szemle 58 (2008) 246.
4. Trócsányi Zoltán: A Standard Modell Higgs-bozonja nyomában az LHC-nál. Fizikai Szemle 57 (2007) 253.
5. Horváth Dezső: Szimmetriák és sértésük a részecskék világában - a paritássértés 50 éve. Fizikai Szemle 57 (2007) 47.

_________________________